Групповая скорость

Плоская однородная монохроматическая волна не может переносить информацию, т.е. являться сигналом, так как она не представляет собой процесс, не изменяющий своего характера в пространстве или времени. Сигналы, несущие информацию, всегда представляются только модулированными колебаниями, импульсными или непрерывными. Изменение поля во времени, т.е., модуляция, служит средством передачи информации.

Любой модулированный сигнал представляет собой спектр частот с определенными амплитудными и фазовыми соотношениями между отдельными частотными составляющими. В дисперсной системе отдельные частотные составляющие распространяются с разными скоростями и испытывают различное затухание. Это нарушает амплитудно-фазовые соотношения в спектре сигнала, и на приемном конце его форма может сильно отличаться от исходной.

Скорость передачи узкополосного сигнала, например сигнала с амплитудной модуляцией, называется групповой скоростью. Во всех случаях, когда дисперсия еще не приводит к существенному искажению сигнала, групповая скорость рассматривается как скорость переноса сигнала. Для ее определения рассмотрим простейший модулированный сигнал − биение двух монохроматических колебаний с равными амплитудами и близкими частотами:

,

, .

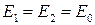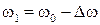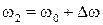Различием между постоянными затухания для двух частот можно пренебречь. Суммарный сигнал в произвольной точке имеет вид:

,

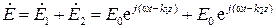где 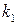, 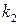− волновые числа на разных частотах 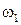, 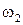. Можно показать, что при не слишком большой полосе частот это выражение принимает вид

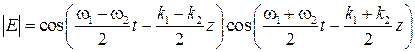
Первый косинус характеризует огибающую биений, а второй − высокочастотное колебание (рисунок 49).

Рисунок 49 − К определению групповой скорости

Амплитуда результирующей волны имеет максимум в максимуме огибающей. Групповую скорость 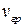определяют как скорость перемещения максимума огибающей, соответствующего максимуму плотности энергии электромагнитного поля. При этом высокочастотный сигнал, заполняющий огибающую, продолжает перемещаться с фазовой скоростью .

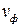Очевидно, что групповая скорость одинакова для всех точек огибающей: найдем эту скорость для какой-либо точки огибающей. Удобно сделать это для точки максимума огибающей.

Обозначим 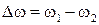, 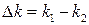. В выражении для колебаний рассмотрим точку, когда первый косинус равен единице и найдем скорость ее перемещения по времени. Это происходит, когда его аргумент равен нулю:

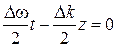
Скорость является производной перемещения по времени. Переходя к пределу, получим

.

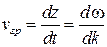Это и является определением групповой скорости. Условием применимости этой формулы и понятия групповой скорости вообще является узость спектра передаваемого сигнала и медленное изменение волнового числа от частоты. При невыполнении этих условий влияние дисперсии становится весьма заметным, сигнал в процессе распространения сильно меняет свою форму и само понятие групповой скорости теряет смысл.

Так как фазовая постоянная в среде с потерями зависит от частоты, то групповая скорость тоже зависит от частоты. В среде без потерь групповая скорость равна фазовой скорости:

.

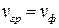В зависимости от типа дисперсии групповая скорость может быть больше или меньше фазовой:

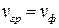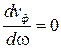, − отсутствие дисперсии

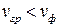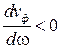, − нормальная дисперсия

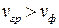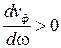, − аномальная дисперсия