Суперпозиция двух линейно поляризованных волн

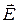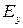Предположим теперь, что волна создается более сложной излучающей структурой и вектор имеет две составляющие и , которые изменяются либо синфазно, либо с некоторым фазовым сдвигом. Вектор 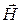в этом случае тоже имеет две составляющие 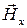и 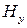, связанные с компонентами 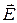. Тогда в общем случае выражение для вектора 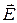плоской волны в среде без потерь записывается в виде

,

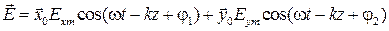где 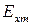и 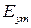− амплитуды составляющих 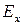и 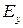соответственно, а 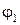и 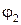− фазы этих составляющих в точке 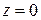при 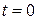. Волну такого типа можно рассматривать как суперпозицию двух плоских линейно поляризованных волн со взаимно перпендикулярными плоскостями поляризаци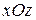и и 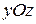, распространяющихся в одном направлении вдоль оси 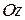. Характер изменения вектора 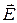с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами 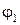, 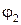и от амплитуд , .

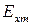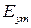Рассмотрим, что произойдет при отдельных частных случаях такой волны. Для этого рассмотрим угол между осью 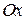и вектором 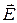в некоторой фиксированной точке пространства 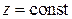. Очевидно, что величина этого угла зависит от соотношения между мгновенными значениями компонент вектора 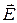(рисунок 51):

,

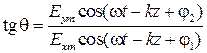то есть, 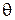зависит от соотношения величин 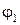, 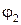и 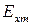, 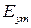и в общем случае меняется со временем. Для получения случая линейной поляризации необходимо, чтобы составляющие вектора 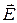были синфазными или противофазными. Положим сначала 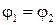, тогда

.

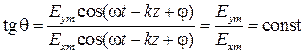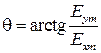В этом случае вектор в любой момент времени лежит в плоскости, проходящей через ось и составляющей угол с плоскостью .

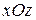Рисунок 52 − Линейно поляризованная волна

Аналогичное явление имеет место также в том случае, когда разность между начальными фазами равна целому числу :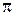

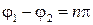, где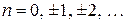

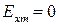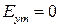Очевидно, что при или линейно поляризованная волна превращается в волну с чисто горизонтальной или чисто вертикальной поляризацией.

Рисунок 53 − Горизонтальная и вертикальная поляризация

Рассмотрим второй частный случай. Пусть амплитуды составляющих 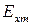и 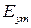равны, а начальные фазы отличаются на :

,

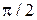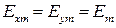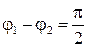
Тогда

,

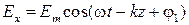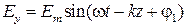
Подставляя эти значения в выражение для угла 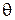, получим:

,

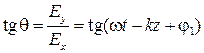откуда следует, что

,

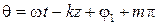где 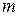− целое число. Это равенство означает, что угол 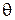в фиксированной точке пространства 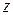увеличивается с течением времени. Величина вектора 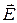при этом остается неизменной:

.

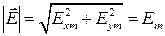Таким образом, в фиксированной точке пространства вектор 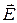, оставаясь неизменным по величине, вращается с угловой частотой 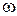вокруг направления оси 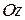. Конец вектора при этом описывает окружность (рисунок 53). Волны такого типа называются волнами с круговой поляризацией.

Рисунок 54 − Круговая поляризация плоской волны

Нетрудно убедиться также, что волна будет иметь круговую поляризацию не только в случае 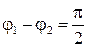, но и

,

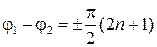где .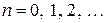

Вдоль направления распространения (вдоль оси 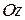) в фиксированный момент времени 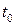в среде без потерь конец вектора 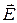описывает винтовую линию с шагом, равным длине волны. Проекция этой линии на плоскость 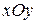образует окружность. С течением времени эта винтовая линия перемещается вдоль оси 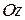по цилиндру с фазовой скоростью .

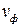В зависимости от направления вращения вектора вокруг оси распространения различают волны с левой и правой круговой поляризацией. В случае правой поляризации вектор 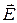вращается по часовой стрелке, если смотреть вдоль направления распространения, а в случае левой круговой поляризации − против стрелки. В рассмотренном примере при 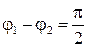волна имеет правую поляризацию. Очевидно, что такая же поляризация будет в случае

, .

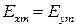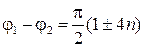В случае

,

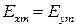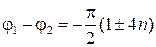
волна имеет левую круговую поляризацию.

Вектор 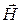однородной волны везде и в любой момент времени перпендикулярен вектору 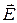и пропорционален ему по величине. Таким образом, в отличие от линейной поляризации, поле бегущей волны с круговой поляризацией в любой момент времени ни в одной точке пространства не равно нулю.

В случае среды с потерями линия, соединяющая концы векторов в один м тот же момент времени в разных точках оси 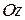, представляет собой спираль с радиусом, который изменяется вдоль оси по закону .

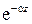В самом общем случае распространения волны, когда 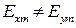конец вектора 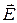будет описывать при фиксированном 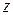и переменном 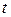в пространстве некий эллипс (рисунок 51). Полуоси эллипса в общем случае не совпадают с осями координат.

Рисунок 55 − Эллиптически поляризованная волна

Для определения эллиптичности поля используется коэффициент эллиптичности, характеризующий отношение малой полуоси эллипса к большой:

.

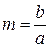При 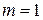эллипс вырождается в окружность, этот случай соответствует электромагнитной волне с круговой поляризацией. Если 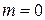, то эллипс вырождается в прямую линию − это линейно поляризованная волна.

При рассмотрении эллиптической и круговой поляризаций нами рассматривалась суперпозиция двух линейно поляризованных волн. Как мы увидели, поле с любым типом поляризации можно представить суммой двух волн, поляризованных линейно в двух ортогональных плоскостях. Можно доказать и обратное: эллиптически или линейно поляризованную волну можно представить в виде суммы двух волн с круговой поляризацией и противоположными направлениями вращения.