Граничные условия для векторов электромагнитного поля

Рассмотренный выше простейший вид электромагнитного волнового процесса − плоская волны − является весьма идеализированным, поскольку здесь предполагается бесконечная протяженность волновых фронтов. В любой практической задаче электромагнитное поле тем или иным способом ограничено в пространстве. Естественными границами могут быть, например, металлические стенки волновода или границы раздела между средами с различными параметрами. Если параметры сред на границе раздела изменяются скачкообразно, то в общем случае компоненты векторов электромагнитного поля также претерпевают разрыв в точках границы. Далее мы найдем связи между векторами поля на границе, которые удовлетворяли бы уравнениям Максвелла.

Математическая постановка данной задачи выглядит следующим образом. Предположим, что две среды с номерами 1 и 2 разделены поверхностью 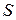. Вблизи от границы раздела известно полное электромагнитное поле, относящееся к области 1. Требуется отыскать электромагнитное поле в такой же окрестности, принадлежащей области 2.

Среда 1 имеет параметры 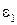, , 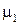, 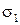среда 2 − соответственно 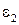, , 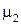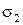. Поскольку на границе эти параметры меняются скачкообразно, то надо ожидать, что компоненты векторов поля при переходе границ раздела сред также будут испытывать разрывы. Тогда векторная линия будет претерпевать излом. Очевидно, что в точках разрыва векторов поля мы лишены возможности применять уравнения Максвелла в их дифференциальной форме. Мы обратимся к интегральной форме этих уравнений и получим важные соотношения, которые называют граничными условиями.

Рисунок 56 − Разложение вектора на тангенциальную и нормальную составляющие

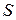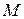Для упрощения решения поставленной задачи векторы электромагнитного поля, рассматриваемые на границе раздела сред, принято разлагать на тангенциальные (касательные) и нормальные составляющие. Для этого выберем на поверхности точку , пусть в этой точке существует вектор некоторого поля 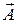. Выделим столь малую окрестность точки 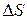, что этот элемент поверхности можно считать плоским. В точке 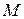построим орт нормали 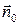по направлению из среды 2 в среду 1. Можно также построить на 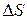сколько угодно касательных к поверхности ортов, выберем из них один 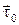, лежащий в плоскости, образованной вектором 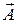и ортом нормали 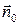. Тогда вектор 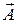может быть представлен в виде компонентов – проекций на выбранные орты:

.

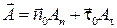Говорят, что вектор поля 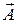разложен на нормальную и тангенциальную (касательную) компоненты.

Далее мы по отдельности рассмотрим поведение тангенциальных и нормальных составляющих векторов на границе раздела сред.