Граничные условия для нормальных составляющих электрического поля

Методика вывода граничных условий и соответствующая иллюстрация остаются здесь совершенно аналогичными тем, что были использованы при выводе условий для нормальных составляющих магнитного поля. Однако за основу принимается не четвертое уравнение Максвелла 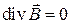, а третье 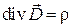. Отсюда возможны два случая.

Первый. Плотность поверхностных электрических зарядов равна нулю. Суммарный электрический заряд 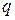, заключенный внутри малой цилиндрической области, при этом равен нулю. В соответствии с теоремой Гаусса

,

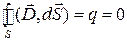откуда по аналогии с предыдущим выводом следует

.

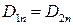Итак, при отсутствии поверхностных электрических зарядов нормальные составляющие векторов электрического смещения на границе раздела двух сред непрерывны, в то время как нормальные составляющие напряженностей электрического поля в общем случае претерпевают скачок:

.

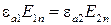Второй случай. На границе раздела равномерно распределен поверхностный электрический заряд с плотностью .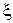

В этом случае, очевидно, стремление к нулю высоты цилиндра 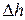не влияет на величину заряда, заключенного внутри цилиндра. Воспользовавшись законом Гаусса, можно записать формулу:

,

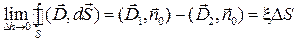откуда следует

.

Это выражение означает, что при наличии заряженной границы раздела нормальные составляющие векторов электрической индукции испытывают скачок, по величине равный плотности поверхностного заряда в исследуемой точке. Физически это обусловлено тем, что заряд, расположенный на поверхности, создает свое собственное поле, ориентированное таким образом, что по одну сторону от границы раздела это поле складывается со внешним полем, а по другую вычитается.