Граничные условия для нормальных составляющих магнитного поля

Данное граничное условие следует из четвертого уравнения Максвелла

,

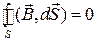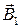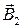т.е. теоремы Гаусса. Обозначим через и векторные поля магнитной индукции в средах 1 и 2 соответственно. Построим пересекающий границу раздела малый цилиндр высотой 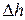(рисунок 57). Основания его параллельны оказавшемуся внутри участку границы 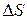, который рассматривается как элемент плоскости. Размер цилиндра будем считать настолько малым, что векторы 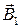и 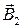не изменяются в пределах площадей .

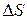Рисунок 57 − Граничные условия для нормальной компоненты магнитного поля

Внешняя нормаль к верхнему основанию направлена по 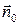, а к нижнему − противоположно. Поэтому поток вектора магнитной индукции через общую поверхность цилиндра запишется следующим образом:

,

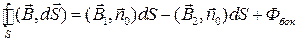где 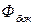− поток через боковую поверхность. Теперь будем неограниченно уменьшать высоту цилиндра 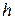, но так, чтобы его основания оставались в разных средах и в пределе 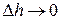совпали с элементом граничной поверхности 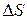. При этом исчезает боковая поверхность цилиндра, а вместе с ней и :

.

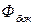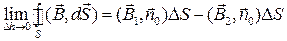Поскольку четвертое уравнение Максвелла, говорящее о непрерывности магнитных силовых линий справедливо всегда, то можно записать

,

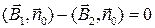или

.

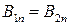Таким образом, нормальные составляющие вектора магнитной индукции на границе раздела двух сред непрерывны. Поскольку 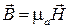, то последнее соотношение может быть записано для напряженности магнитного поля:

.

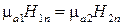Из этого следует, что в общем случае напряженность магнитного поля на границе раздела сред испытывает скачок.