Граничные условия для тангенциальных составляющих магнитного поля

Задача о поведении на границе раздела тангенциальных составляющих магнитного поля решается на основе второго уравнения Максвелла (закон полного тока) в интегральной формулировке:

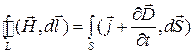
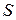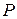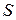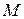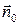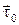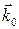Проведем через граничную поверхность плоскость , проходящую через нормаль к . Введем в исследуемой точке три взаимно ортогональных вектора , и . Векторы 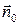, 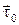по прежнему являются единичными векторами нормального и тангенциального направлений и лежат в плоскости 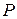, а 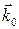образует с ней нормаль.

Выделим в окрестности точки 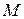малый прямоугольный контур, целиком лежащий в плоскости 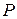таким образом, что две его стороны пересекают границу раздела, а две лежат по разные стороны от границы раздела. Обозначим длину сторон контура 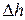и 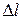. Зададим направление обхода контура по направлению орта 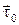(против часовой стрелки, наблюдая с конца орта ).

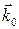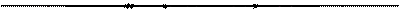
Рисунок 58 − К выводу граничных условий для тангенциальных составляющих электрического поля

В обоих областях, разделяемых границей, протекают некоторые токи, которые могут включать как токи проводимости, так и токи смещения. Применим к контуру второе уравнение Максвелла, причем будем считать, что размеры контура достаточно малы для того, чтобы считать в поле в его пределах постоянным: 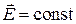. В результате получим

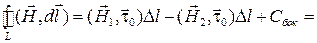
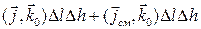
Здесь первые два члена получены вычислением циркуляции вектора 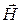по участкам контура 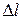, так как направление обхода по ним противоположно, то и знак членов отличается. 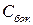− циркуляция вектора напряженности магнитного поля по боковым сторонам контура длиной .

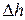Далее снова нужно рассмотреть два случая.

Первый случай. Электродинамические параметры обеих граничащих сред являются величинами конечными, т.е., не равными бесконечности. Отсюда непосредственно следует конечное значение векторов плотности токов проводимости и смещения.

Теперь совершим предельный переход, устремляя высоту контура 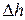к нулю. В силу предположения о конечности векторов тока проводимости и смещения будем иметь

.

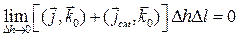Кроме того, циркуляция вектора 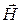по боковым сторонам контура также будет равна нулю 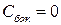. С учетом сказанного будем иметь:

,

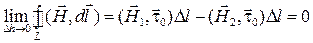или

.

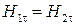Таким образом, при конечных значениях электродинамических параметров сред тангенциальные составляющие векторов напряженности магнитного поля непрерывны. Отсюда сразу следует, что тангенциальные составляющие векторов магнитной индукции терпят разрыв:

.

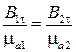Рассмотрим теперь второй случай, считая, что проводимость одной из граничащих сред бесконечна.

Положим, например, что бесконечна проводимость второй среды 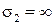. Подобное предположение делает неприменимой формулу 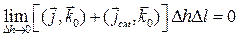. Дело в том, то при бесконечно большой проводимости среды толщина скин-слоя (глубина проникновения электромагнитных волн) равна нулю на любой частоте. В результате токи проводимости протекают по поверхностной пленке нулевой толщины, и предельный переход даст отличный от нуля результат.

Для этого случая вводят понятие вектора плотности поверхностного тока 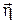. Принцип введения этого вектора показан на рисунке 59 .

Рисунок 59 − Поверхностный ток

Прежде всего проведем единичный вектор, касательный к линиям тока в данной точке. Этот вектор обозначается как 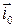. Затем находится величина тока 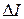, протекающего через отрезок 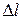, перпендикулярный вектору 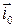. Плотность поверхностного тока определяется как

.

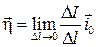Теперь закон полного тока для контура можно записать в виде

.

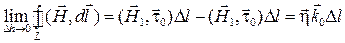Далее следует учесть, что внутри идеального проводника все составляющие электромагнитного поля должны равняться нулю. Так как бесконечно проводящей принята вторая среда, то поэтому 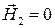и получим

.

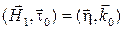Это выражение является граничным условием для тангенциальной составляющей вектора напряженности магнитного поля на границе с идеальным металлом. Данная формула позволяет решить важную для практики задачу − найти плотность поверхностного тока по известному магнитному полю на границе идеального проводника. С учетом того, что

,

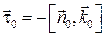можно записать

.

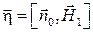Таким образом, поверхностный ток на границе раздела с идеальным металлом протекает в направлении, перпендикулярном вектору 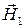, и численно равен напряженности магнитного поля.