Плоские волны

Рассмотрим безграничное трехмерное пространство с декартовой системой координат, в каждой точке которого задана некоторая величина 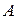, физическая природа которой безразлична. Пусть эта величина во времени и пространстве изменяется по закону

.

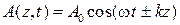При этом говорят, что в пространстве существует монохроматическая плоская волна. Аргумент косинуса, т.е. 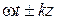, называемый обычно фазой волны, является функцией времени 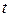и пространственной координаты 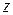. Если зафиксировать 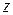, то величина 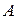принимает те же самые значения через промежутки времени, кратные периоду 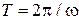. Если же фиксировано время, то величина 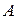изменяется периодически вдоль оси 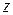с периодом 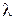, называемом длиной волны. 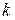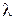Легко видеть, что величины и связаны друг с другом:

.

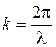Величина 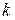служит важнейшей характеристикой волнового процесса и носит название постоянной распространения волны. Употребляются также термины фазовая постоянная и волновое число, а вместо символа 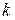используется 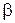. Физический смысл волнового числа состоит в том, что оно указывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.

Наличие двух возможных знаков в формуле, описывающей плоскую волну, связано с тем, что плоские волны могут распространяться в двух направлениях. Назовем поверхность, удовлетворяющую условию

,

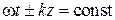волновым фронтом плоской волны. Очевидно, что в рассматриваемом случае волновые фронты представляют собой бесконечные плоскости, перпендикулярные оси 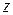и перемещающиеся в пространстве со скоростью

,

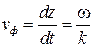носящей название фазовой скорости. Фазовая скорость − это скорость, с которой должна перемещаться точка наблюдения, чтобы фаза поля в ней оставалась неизменной. Поскольку время изменяется всегда в одном направлении, то уравнение

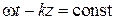
соответствует фронту волны, распространяющейся в направлении положительной оси 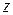. Изменение знака в фазе волны ведет к изменению направления ее распространения.

Рисунок 42 − Плоская волна

Введем комплексные амплитуды плоских волн. В соответствии с методом комплексных амплитуд будем иметь для волны, распространяющейся в положительном направлении

,

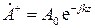а для волны, идущей в противоположную сторону,

.

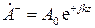Распространение волн в любой реальной среде неизбежно сопровождается уменьшением их амплитуды за счет тепловых потерь. Закон затухания легко найти из следующих простых соображений. Предположим, что в начальной плоскости 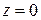амплитуда волны имеет исходную величину 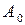, условно принимаемую за 100%. Положим далее, что при прохождении 1 м пути амплитуда падает на 10%, т.е. 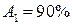. Легко найти, что 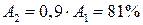, 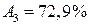и т.д. Общая закономерность имеет вид

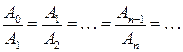
Из алгебры известно, что именно таким свойством обладает показательная функция, т.е. в общем виде можно записать соотношение пропорциональности

.

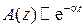Рисунок 43 − Спадание амплитуды волны при распространении в среде с потерями

Здесь 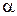носит название постоянной затухания волны. Величины 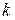и 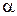можно объединить, введя комплексную постоянную распространения :

.

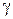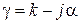Итак, вещественная часть 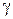определяет закон изменения фазы в распространяющейся волне, в то время как мнимая часть характеризует затухание.