Уравнения Гельмгольца. Волновой характер электромагнитного поля
Одним из важнейших результатов, полученных Максвеллом, явилось доказательство волновой природы электромагнитного поля. Уже упоминалось о том, что изменение во времени электрического поля приводит к возникновению магнитного поля, неоднородного в пространстве, и наоборот. Физическая картина здесь напоминает процесс обмена энергией между электрическим и магнитным полем в обычном колебательном контуре. Поэтому можно ожидать, что электромагнитный процесс в самом общем случае представляет собой также некоторые колебания. Принципиальная разница здесь заключается в том, что колебания электромагнитного поля должны рассматриваться одновременно во всех точках пространства. В физике колебательное движение непрерывной среды принято называть волновым процессом.
Докажем волновой характер электромагнитного поля математически, сведя уравнения Максвелла к другим уравнениям, которые заведомо описывают волновой процесс.
Рассмотрим электромагнитное поле в некоторой области пространства, где плотность зарядов отсутствует, т.е. 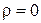 . Плотность сторонних электрических токов также предполагается равной нулю.
. Плотность сторонних электрических токов также предполагается равной нулю.
Выпишем первые два уравнения из общей системы уравнений Максвелла для комплексных амплитуд в виде:
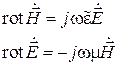
Эти два уравнения могут быть сведены к одному. Для этого применим операцию rot к левой и правой частям второго уравнения, а затем выразим полученную правую часть через второе уравнение:
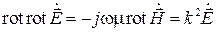
Здесь 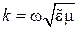 − в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величины
− в общем случае комплексное число, являющееся, как будет показано, постоянной распространения электромагнитной волны. В литературе для величины 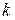 можно встретить также названия фазовая постоянная или волновое число.
можно встретить также названия фазовая постоянная или волновое число.
Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождеством векторного анализа:
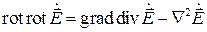 .
.
Здесь 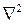 (набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие оператора
(набла квадрат) − векторный дифференциальный оператор второго порядка, конкретная форма которого полностью определяется той координатной системой, в которой производятся вычисления. Для декартовой системы координат действие оператора 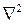 сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа
сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа
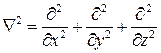 .
.
Если воспользоваться законом Гаусса, который в соответствии с принятым условием 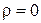 обеспечивает
обеспечивает 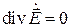 , то уравнение может быть переписано в следующем простом виде:
, то уравнение может быть переписано в следующем простом виде:
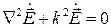
Пользуясь симметрией уравнений Максвелла, совершенно аналогично получаем также уравнение относительно векторного поля 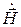 :
:
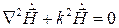 .
.
Эти два уравнения в математической физике носят название уравнений Гельмгольца. Математически можно показать, что эти уравнения описывают стационарные волновые процессы, т.е., распространение в пространстве волн с некоторой постоянной частотой.
Таким образом, получен фундаментальный вывод теории Максвелла − переменность во времени электрических или магнитных полей приводит к распространению в пространстве электромагнитных волн.
В координатной форме уравнения Гельмгольца записываются следующим образом
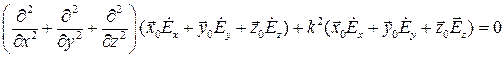
или
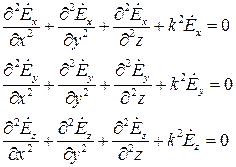 .
.
Решение такой системы значительно упрощается в тех частных случаях, когда поле не имеет каких-либо составляющих, например, 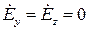 , а также тогда, когда поле постоянно в каких-либо плоскостях, например
, а также тогда, когда поле постоянно в каких-либо плоскостях, например 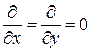 .
.
Дата добавления: 2015-10-19; просмотров: 2335;
