Определение необходимой численности выборки
Средняя квадратическая (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки, всегда связано с увеличением объема выборки. В этой связи уже на стадии организации выборочного наблюдения приходиться решать вопрос, о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдения. Рассмотрим формулу предельной ошибки выборки для случая простой случайной повторной выборки.
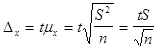
отсюда 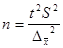 (5.1.)
(5.1.)
при проектировании выборочного наблюдения предполагается заранее заданной величина допустимой ошибки выборки в соответствии с задачами конкретного исследования.
Величина 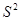 , характеризующая дисперсию признака в генеральной совокупности, зачастую бывает неизвестна. Поэтому используют приближенные способы оценки генеральной дисперсии.
, характеризующая дисперсию признака в генеральной совокупности, зачастую бывает неизвестна. Поэтому используют приближенные способы оценки генеральной дисперсии.
1) можно провести “пробное” обследование (обычно небольшого объема), на базе которого определяется величина дисперсии признака
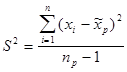
где 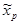 - средняя арифметическая по результатам пробного обследования;
- средняя арифметическая по результатам пробного обследования;
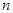 проб. - число единиц, попавших в пробное обследование.
проб. - число единиц, попавших в пробное обследование.
По данным нескольких пробных обследований выбирается наибольшее значение дисперсии.
2) можно использовать данные прошлых выборочных обследований, проводившихся в аналогичных целях.
3) если распределение признака в генеральной совокупности может быть отнесено к нормальному закону распределения, то размах вариации примерно равен 6S, т.е. R»6S откуда S»1¤6 R, где R=Xmax-Xmin.
При проведении социально-экономических исследований, как правило, можно с достаточной точностью указать максимально и минимально возможные значения признака в исследуемой совокупности.
Например, сколько операционистов нужно обследовать в банках региона, чтобы получить характеристику среднего уровня оплаты труда этой категории работников банков в регионе? Положим, нам известно, что разница между наивысшем и наименьшем уровнем оплаты труда операциониста в регионе составляет 300 руб. Для нормального распределения в промежуток 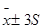 включается 99,7% всех вариантов значений признака, а это означает применительно к рассматриваемой задаче, что 300 руб. примерно равно шести средним квадратическим отклонениям (300»6S). Поэтому примерная оценка среднего квадратического отклонения заработной платы в генеральной совокупности операционистов региона составит 50 руб.
включается 99,7% всех вариантов значений признака, а это означает применительно к рассматриваемой задаче, что 300 руб. примерно равно шести средним квадратическим отклонениям (300»6S). Поэтому примерная оценка среднего квадратического отклонения заработной платы в генеральной совокупности операционистов региона составит 50 руб. 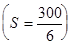 . Для дальнейших расчетов достаточно, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 10 руб. Тогда, зная что S=50 руб., а t=2, и используя формулу (5.1.) для определения необходимого объема выборки получим:
. Для дальнейших расчетов достаточно, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 10 руб. Тогда, зная что S=50 руб., а t=2, и используя формулу (5.1.) для определения необходимого объема выборки получим:
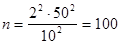 человек
человек
Таким образом, при заданных условиях нужно обследовать размер заработной платы у 100 операционистов региона.
В связи с тем, что генеральная дисперсия оценивается приближенно, рекомендуется величину объема выборки, рассчитанную по формуле (5.1.), округлять в большую сторону. Эту же формулу рекомендуется использовать для определения объема выборки и в тех случаях когда
проводится случайная бесповторная выборка, так как всегда необходим некоторый “запас” числа обследованных единиц для обеспечения требуемой точности результатов.
При определении по материалам выборки доли признака, а не средней его величины, объем выборочной совокупности определится по следующим формулам:
а) для повторного отбора
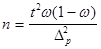 (5.2.)
(5.2.)
б) для бесповторного отбора
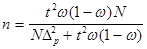 (5.3.)
(5.3.)
Для случая, когда частость даже приблизительно неизвестна, можно произвести примерный расчет численности выборки, вводя в расчет максимальную величину дисперсии доли, равную 0,25:
а) для повторного отбора
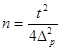 (5.4.)
(5.4.)
б) для бесповторного отбора
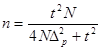 (5.5.)
(5.5.)
Очень часто цель выборочного наблюдения сводится к изучению различных признаков, характеризующих данную совокупность. Причем зачастую по степени колеблемости эти признаки могут сильно отличаться друг от друга. Кроме того, для различных признаков может требоваться разная степень точности. В таких случаях при определении необходимого объема выборки следует ориентироваться на тот признак, который при наибольшей колеблемости обладает наименьшей величиной допустимой ошибки.
Например, при проведении выборочного наблюдения требуется определить средний вес изделия и долю изделий первого сорта в совокупности объемом 5000 ед. Устанавливаем требуемую точность: для среднего веса - 1г; для доли - 5%. По данным сплошного обследования изделий первой партии, состоящей из 100 единиц, определим дисперсию веса, равную 36, и дисперсию доли, равную 0,05. Требуется определить необходимую численность случайной бесповторной выборки, обеспечивающей заданную
точность наблюдения с вероятностью 0,954.
Исходные данные:
а) для определения n, обеспечивающего заданную точность оценки среднего веса изделия.
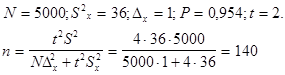
б) для определения необходимого объема выборки, обеспечивающего требуемую точность в определении доли изделий первого сорта, располагаем такими данными;
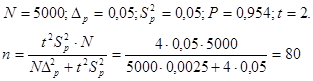
Очевидно, что число изделий, обеспечивающее требуемую точность результатов выборочного наблюдения для определения доли изделий первого сорта недостаточно, чтобы обеспечить требуемую точность при определении среднего веса изделий. Поэтому следует произвести отбор из генеральной совокупности не менее 140 изделий.
В целом формула предельной ошибки выборочной средней (доли), позволяет решать следующие три группы задач:
1) определять предел возможной ошибки средней (доли), т.е. величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности.
2) определять необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой наперед заданной величины.
3) определять вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.
Для решения всех перечисленных задач необходимо знать дисперсию признака в генеральной совокупности 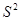 и в случае бесповторной выборки ее объем N.
и в случае бесповторной выборки ее объем N.
В целях упрощения определения объема выборки можно воспользоваться заранее рассчитанными таблицами, в которых указывается необходимое число наблюдений при данной величине доверительной вероятности и допустимой ошибке. Например, при определении доли признака в исследуемой совокупности можно воспользоваться такой таблицей.
Таблица 5.3.
| Доверительная | Предельная ошибка, % | |||
| вероятность | ||||
| 0,90 | ||||
| 0,95 | ||||
| 0,99 | ||||
| 0,997 |
Необходимое число наблюдений рассчитано исходя из формулы предельной ошибки повторного отбора при максимальной величине дисперсии доли равной 0,25. Из таблицы 5.3. видно, что для того, чтобы гарантировать с вероятностью 0,95 величину отклонения от генеральной доли, не превышающую 10%, нужно обследовать 96 единиц. Если предельную ошибку уменьшить до 5%, то нужно подвергнуть обследованию уже 384 единицы, т.е. в четыре раза больше, а для обеспечения с вероятностью 0,95 точности в 1% при определении доли нужно обследовать уже 9603 единицы. Таким образом, таблица позволяет исследователю сделать вывод о целесообразности увеличения объема выборки, а следовательно, и о целесообразности дополнительных затрат, обеспечивающих то или иное повышение точности.
Дата добавления: 2015-09-02; просмотров: 2947;
