Величины отклонения Стьюдента t
(краткая выдержка)
| 0,95 | 0,99 | 0,997 | |
| 2,776 | 4,604 | 6,435 | |
| 2,262 | 3,250 | 4,024 | |
| 2,145 | 2,977 | 3,583 | |
| 2,086 | 2,845 | 3,376 | |
| 2,064 | 2,797 | 3,302 | |
| 2,048 | 2,763 | 3,250 |
Приведем пример, иллюстрирующий практическое применение распределения Стьюдента.
Оздоровительный центр, рекламируя свои услуги, предлагает клиентам за короткий срок снижение веса до 10 кг. По результатам выборочного обследования 15 женщин, воспользовавшихся услугами центра, были получены следующие данные о снижении их веса:
| 10,2 | 7,6 | 6,1 | 8,4 | 6,0 | 5,7 | 13,7 | 6,9 | 5,2 | 6,1 | 5,0 | 3,7 | 4,7 | 3,6 | 3,2 |
Выборочная средняя составляет 6,41 кг (`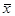 
=96,1/15=6,41 кг.), т.е среднее снижение веса у обследованных женщин составило 6,41 кг. Выборочная дисперсия равна 7,061 ( 
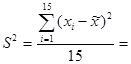7,061). Следовательно, средняя квадратическая ошибка выборки составляет 0,71 кг.
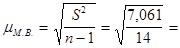0,71 кг
Оценим с вероятностью 0,99 предел возможных расхождений выборочной средней и генеральной средней. Так как число степеней свободы равно 14(К=n-1=15-1), то по табл.5.2. находим, что значение t, соответствующее вероятности 0,99, равно 2,977.
Тогда с вероятностью 0,99 можно предполагать, что ошибка выборочной средней будет не больше 2,114 кг (2,977x0,71), а снижение веса пациентов оздоровительного центра будет находиться в пределах от 4,3 до 8,52 кг (6,41±2,11). Следовательно, указанное в рекламе снижение веса на 10 кг имеет столь малую вероятность, что считается событием практически невозможным.
Дата добавления: 2015-09-02; просмотров: 1337;