Аналитический метод отделения корней
Процесс отделения корней начинается с установления знаков функции 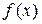 в граничных точках
в граничных точках 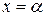 и
и 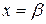 области ее существования. Затем определяются знаки функции
области ее существования. Затем определяются знаки функции 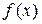 в ряде промежуточных точек
в ряде промежуточных точек 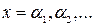 , выбор которых учитывает особенности функции
, выбор которых учитывает особенности функции 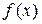 . (Имеются в виду точки, где функция имеет экстремум или разрыв) Если окажется, что
. (Имеются в виду точки, где функция имеет экстремум или разрыв) Если окажется, что 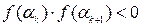 , то в силу теоремы в интервале
, то в силу теоремы в интервале 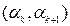 существует корень уравнения
существует корень уравнения 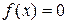 . Можно сузить полученные промежутки методом простой подстановки значений в уравнение.
. Можно сузить полученные промежутки методом простой подстановки значений в уравнение.
Пример2.1. Отделить корни уравнения
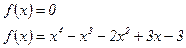
Найдем корни производной

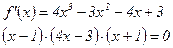 ,
,
 x1=1 x2=0.75 x3=1
x1=1 x2=0.75 x3=1
Составим таблицу. В первой строке поместим в порядке возрастания концы интервала и точки экстремумов, во второй знаки функции в этих точках.
| х | -∞ | -1 | 0.75 | ∞ | |
| Sign f(x) | + | - | - | - | + |
Уравнение имеет два корня. 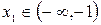 ,
, 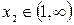 . Уменьшим промежутки, в которых находятся корни:
. Уменьшим промежутки, в которых находятся корни:
| х | -∞ | -2 | -1 | 0.75 | ∞ | ||
| Sign f(x) | + | + | - | - | - | + | + |
Следовательно, 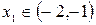 ,
, 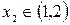 .
.
Дата добавления: 2015-10-09; просмотров: 1464;
