Формы записи данных.

Если а — точное значение некоторой величины а, а * — известное приближение к нему, то абсолютной погрешностью приближенного значения а* называют обычно некоторую величину Δ(а*), про которую известно, что

|а* - а| ≤ Δ(а*)

Относительной погрешностью приближенного значения называют некоторую величину δ(а*), про которую известно, что

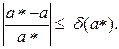
Относительную погрешность часто выражают в процентах. Если а — известное число, например π, то иногда говорят об абсолютной Δ (а) и относительной δ(а) погрешностях задания этого числа: числа Δ(а) и δ(а) называют соответственно абсолютной и относительной погрешностью числа а.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 1.1. У чисел а* = 0,07045, а* = 0,07045000 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором — 7.

Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 1.2. а* = 0,06045, Δ(а*)=0,000003;

а* = 0,06045000, Δ(а*)=0,0000007;

подчеркнутые цифры являются верными.

Уславливаются называть значащую цифру верной в строгом смысле, если абсолютная погрешность не превосходит половины единиц разряда, соответствующих этой цифре.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Пример 1.3. При а* = 0,03045, Δ(а*)= 0,000003 число а* записано со всеми верными цифрами.

Иногда употребляется термин число верных цифр после запятой: подсчитывается число цифр после запятой от первой цифры до последней верной цифры. В последнем примере это число равно 5.

Довольно часто информация о некоторой величине задается пределами ее измерения:

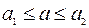, (1.2)

например, .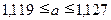

Принято записывать эти пределы с одинаковым числом знаков после запятой, Так как обычно достаточно грубого представления о погрешности, то в числах а₁, а₂ часто берут столько значащих десятичных цифр, сколько нужно, чтобы разность а₁ — а₂ содержала одну-две значащие цифр. Абсолютную или относительную погрешность обычно записывают в виде числа, содержащего одну или две значащих цифры. Информацию о том, что, а* является приближенным значением числа а с абсолютной погрешностью Δ (а*), иногда записывают в виде

а = а*± Δ(а*), (1.3)

числа а* и Δ(а*) принято записывать с одинаковым числом знаков после запятой. Например, записи

а = 1,132 ±0,004, а = 1,132 ±4*10^-3

относятся к общепринятым и означают, что

1,132 - 0,004 < а < 1,132 + 0,004.

Соответственно информацию о том, что а* является приближенным значением числа а с относительной погрешностью (а*), записывают в виде

a = a*(1± δ(a*)). (1.4)

Например, записи

а = 1,132 (1 ± 0,004), а = 1,132(1 ± 4 *10^-3), а = 1,132(1 ± 0,4℅)

означают, что

(1 - 0,004)1,132 < а < (1 + 0,004)1,132.

При переходе от одной из форм записи к другой надо следить, чтобы пределы измерения, указываемые новой формой записи, были шире старых, иначе такой переход будет незаконным. Например, при переходе от (1.2) к (1.3) должны выполняться неравенства

a*- Δ(a*) 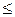a₁, a₂ 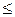a* + Δ(a*),

при переходе от (1.3) к (1.4) — неравенства

а*(1 - δ (а*)) 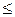а* - Δ (а*), а* + Δ (а*) 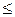а*(1 + δ(а*)),

при переходе от (1,4) к (1.3) должны выполняться противоположные неравенства (пределы всегда расширяются!).

Следует различать принятую нами выше формально математическую и обиходную терминологии в рассуждении о величине погрешности. Если в постановке задачи говорится, что требуется найти решение с погрешностью 10^-2, то чаще всего не имеется в виду обязательность этого требования. Предполагается лишь, что погрешность имеет такой порядок. Если, например, решение будет найдено с погрешностью 2-10^-2, то такой результат, также удовлетворителен.