Метод половинного деления. Пусть уравнение (2.1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0

Пусть уравнение (2.1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [a,b] пополам точкой x₁=(а+b)/2. Если f(x₁)≠0 , то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [a₁,b₁] и снова разделим отрезок [a₁,b₁] пополам точкой x₂=( a₁+ b₁)/2 и т. д. В результате на каком-то этапе получим или точный корень уравнения(2.1) или бесконечную последовательность вложенных друг в друга отрезков [a₁,b₁], [a₂,b₂],… [a_n,b_n],…таких, что

f(a_n)·f(b_n)<0, (n=1,2,…) (2.2)

b_n - a_n=2 ^-n·(b-a). (2.3)

Так как левые концы a₁, a₂,… ,a_n образуют монотонную неубывающую ограниченную последовательность, а правые концы b₁ b₂,…,b_n образуют монотонную невозрастающую ограниченную последовательность, а расстояние между ними в силу (2.2) стремится к нулю, то у последовательностей существует общий предел . Число ξ, которое является общим пределом последовательностей {a_n} и {b_n}, точный корень уравнения (2.1). Оценим погрешность решения на n-м шаге. Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε.

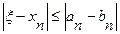
В качестве ответа возьмем середину отрезка [a_n,b_n].

.

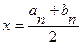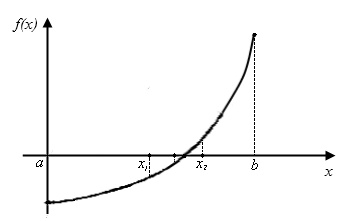
Рис.2.2. К объяснению метода половинного деления

Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объём вычислений.

Пример 2.3. Найти, используя пакет Matchcad, методом половинного деления корень уравнения x⁴-x³-2x²+3x-3=0 на промежутке [1,2]

Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε, и значение корня на этом промежутке, если на концах отрезка [a,b] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.

Метод легко реализуется на компьютере. Далее приводится листинг программы, написанной на языке, встроенном в систему Mathcad.

Рис. 2.3. Листинг программы в Mathcad, реализующей метод половинного деления для примера 2.3