Вычислительная погрешность
Далее для краткости будем обозначать абсолютную погрешность числа x как Δx относительную погрешность как δХ .
1. Погрешность суммирования чисел х±Δх, у± Δy
Абсолютная: погрешность:
Δz = (x± Δx)+(y± Δy)=(x + y) ±(Δx± Δy)
Относительная погрешность:
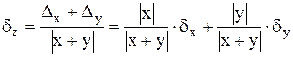
2. Погрешность вычитания чисел х±Δх, у± ΔY
Абсолютная: погрешность:
Δz = (x± Δx)-(y± Δy)=(x + y) ±(Δx± Δy)
Относительная погрешность:
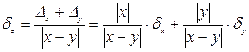
3. Погрешность умножения чисел х±Δх, у± Δy
Абсолютная: погрешность:
z = (x± Δx) (y± Δy)=xּy± yּΔx ±xּΔy± ΔxּΔy = xּy± yּΔx ±xּΔy
Относительная погрешность:
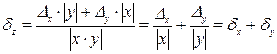
4. Погрешность деления чисел х±Δх, у± Δy
Абсолютная: погрешность:
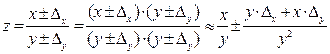
Относительная погрешность:
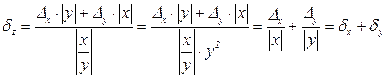
5. Погрешность функции, зависящей от одной переменной.
Абсолютная: погрешность:
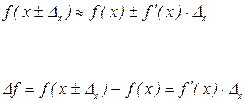
Относительная погрешность:
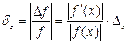 .
.
Дата добавления: 2015-10-09; просмотров: 1339;
