Оптимальная численность выборки.
При организации выборочного обследования следует иметь в виду, что размер ошибки выборки зависит от численности выборочной совокупности n. Вспомним, что 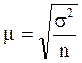 , т.е. средняя ошибка выборки пропорциональна
, т.е. средняя ошибка выборки пропорциональна 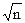 , т.е. при увеличении численности выборки в 4 раза, ошибка уменьшится вдвое. Увеличивая n можно свести ошибку к min. При n
, т.е. при увеличении численности выборки в 4 раза, ошибка уменьшится вдвое. Увеличивая n можно свести ошибку к min. При n 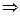 N,
N, 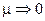 .
.
Так как при проведении выборочного наблюдения определение характеристик выборки в ряде случаев сопровождается разрушением обследуемых образцов, то нормы отбора должны быть минимальны, так же не следует забывать об основном преимуществе несплошного наблюдения ( min затрат и времени ). Повышение процента выборки ведет к увеличению объема исследуемой работы. В то же время, если в выборку взять недостаточное количество проб, то результаты исследования будут содержать большие погрешности. Все это необходимо учитывать при организации выборочного обследования.
Определение необходимой численности выборки основывается на формуле предельной ошибки выборки (при повторном отборе).
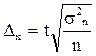
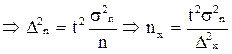
Решаем это равенство относительно n, в результате получаем численность выборки при расчете средней величины количественного признака.
Аналогично выводится формула для расчета численности выборки при выборочном обследовании доли альтернативного признака (обозначим 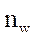 ):
):
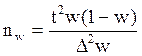
Вывод формул для определения численности выборки при бесповторном отборе аналогичен.
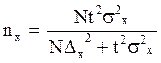
Дата добавления: 2015-10-09; просмотров: 1057;
