Сенсорная система в свете теории информации
С точки зрения его функции нервное волокно можно сравнить с кабелем, передающим информацию. Подход инженеров связи-теорию ин-
|
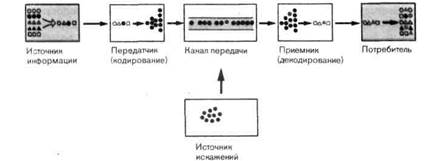
Рис. 2-17. Схема, иллюстрирующая понятия и термины теории информации.
формации-можно применить также и к нервной системе. Эту область знаний в совокупности с теорией управления часто называют кибернетикой; ее применение к биологии называют биокибернетикой, особенно в Европе, в США такие общие термины используются реже.
Элементы теории информации.Фундаментальная идея, из которой развилась теория информации, представлена в виде блок-схемы на рис. 2-17. Здесь выделены те функциональные компоненты, которые принимают участие в передаче информации: источник информации, передатчик, канал передачи, приемник, потребитель и источник помех, который в данном примере действует на канал передачи. Это простое расчленение можно применить ко всем видам передачи информации как в технике, так и в биологии. Теория информации может дать количественную меру информации, что позволяет выводить утверждения, помогающие описывать и сравнивать системы передачи информации.
Чтобы передавать информацию, нужны символы (например, буквы или цифры); в определенной степени они задаются или определяются источником информации. Эти знаки кодируются в передатчике, обычно преобразуясь в другие виды сигналов, более подходящие для передачи (например, частотно-модулированные электромагнитные волны в случае ЧМ-радиосвязи). Кодирование -это общий термин, используемый .для такого преобразования,при котором сохраняется однозначная связь между элементами двух наборов знакои; примером кодирования является перевод букв алфавита в знаки азбуки Морзе. В приемнике переданная информация декодируется и направляется потребителю.
В теории информации особое внимание уделяется влиянию помех. Помехи могут возникать в передатчике (в процессе кодирования), в канале передачи и в приемнике (при декодировании). Такие источники помех представлены на рис. 2-17 как один элемент, действующий на канал передачи. Одной лз задач теории информации является нахождение таких процедур кодирования, которые защищают информацию от разрушающего действия помех.
Как можно измерять информацию? В теории информации термин
 «информация» применяется только к тем характеристикам сообщений, которые поддаются численной оценке и могут описываться математическими формулами. Следующий пример показывает, откуда возникает такое использование этого термина.
«информация» применяется только к тем характеристикам сообщений, которые поддаются численной оценке и могут описываться математическими формулами. Следующий пример показывает, откуда возникает такое использование этого термина.
Если вы бросите одну игральную кость из пары, то с одинаковой вероятностью может выпасть одно из шести чисел. До бросания мы знаем только то, что результатом будет одно из шести определенных чисел. Акт бросания устраняет эту неопределенность измеримым образом, что мы можем использовать для определения информационного содержания броска. Заметим, что каждое такое событие, т.е. каждое бросание кости с шестью гранями, будет иметь одинаковое информационное содержание. Событие другого типа-подбрасывание монеты (где есть только два возможных результата) будет иметь другое информационное содержание. В общем случае можно сказать, что: информационное содержание события-это количественная мера уменьшения неопределенности наших знаний о ситуации благодаря знанию исхода события. Заметьте, что передача символов от источника к потребителю имеет точную аналогию с вышеприведенными примерами-тут тоже имеется измеримое уменьшение априорной неопределенности.
Легко видеть, что это уменьшение неопределенности сведений об исходе события тем больше, чем меньше вероятность р получения каждого исхода; бросание кости (р = 1/6) устраняет большую неопределенность, чем подбрасывание монеты (р = 1/2). В связи с этим количество информации / имеет смысл определить через величину, обратную р, т. е. через 1/р. Разумным дополнительным условием для измерения информации является требование, чтобы в случае события с одним возможным исходом, который обязательно наступит и, значит, имеет вероятность 1, количество информации равнялось бы нулю. Это условие можно выполнить, используя логарифмическую функцию от 1/р, поскольку log 1 = 0.
Эти рассуждения поясняют, почему количество информации в одном событии (или сообщении, состоящем из одного символа, выбранного из нескольких равновероятных) было определено как
I = log(l/p). [2-5]
В этом определении используют логарифм по основанию 2 (записывая его в виде log2), поскольку тогда ситуация с р = 1/2 будет давать 1 ед. информации. Таким образом, [2-5] можно следующим образом переписать для определения количества информации / в событии, имеющем равновозможные исходы с вероятностью р:
I = log2(l/p). [2-6]
Для игры в кости информационное содержание каждого броска одной игральной кости теперь можно оценить численно: I = log2 [1 (1/6)] = 2,58 бит. Что такое «бит», мы узнаем позже. Поскольку логарифмические линейки и карманные калькуляторы обычно не
дают возможности непосредственно определять функцию log2, полезно знать формулу перевода: log2 п = log10 n/log10 2 = 3,32• log10 n.
Вводя меру информации, мы начали с предположения, что все состояния источника информации могут иметь место с одинаковой вероятностью р, как, например, в случае игральных костей. Это предположение является упрощением; обычно отдельные знаки, или состояния, источника информации не равновероятны.
Примером случая неравной вероятности могут служить буквы алфавита, которые встречаются в тексте с разными частотами (вероятностями). Читатель может легко убедиться в этом самостоятельно; в англий-ском'тексте, например, самая распространенная буква-е. Общий случай неравных вероятностей выходит за рамки данного вводного рассмотрения меры информации; интересующиеся читатели могут найти дополнительную литературу по приведенному списку.
Остановившись на частном случае равных вероятностей, заметим, однако, что [2-6] можно записать в другом виде; если и-общее число возможных символов, или состояний источника, справедливо равенство р = \/п. Для игральной кости п = 6. Выражая через п количество информации при передаче одного символа, получим
/ = log2n. [2-7]
Это значит, что содержание информации в таком сообщении равно логарифму по основанию 2 числа п всех возможных символов, которые могут быть переданы. Мы применим это соотношение в нейрофизиологии (см. далее).
Конечно, субъективная ценность единицы информации для получателя зависит от многих факторов, не включенных в рассмотренную выше количественную меру информации. Например, при игре в кости субъективная цена, которую игрок назначает разным числам, может варьировать в зависимости от бессознательной мотивации, его отношений с другими партнерами, того, последний ли доллар он сейчас ставит, и т.д. Изучение таких аспектов символьной информации часто называют семантикой.
Двоичные и недвоичные знаки; бит.Как подчеркивалось выше, передача информации требует набора символов, из которых передающий информацию может делать выбор. В простейшем случае набор состоит всего из двух символов, называемых двоичными, или бинарными (например, двух цифр: 0 и 1). Используя их, передающий информацию может посылать сообщения о выборе из двух возможных вариантов (например, «да» или «нет»). Двоичные системы особенно удобны с технической точки зрения; примерами их реализации являются свет-темнота, смена положений тумблера, наличие и отсутствие отверстия в перфокарте. Это одна из причин, по которой в качестве единицы информации было выбрано информационное содержание акта, определяющего один двоичный символ. Этот выбор уже подразумевался в [2-6] и [2-7], так
как log2 2=1. Количество информации, которое передается в сообщении, содержащем один из двух равновероятных двоичных символов, называется одним битом.
Один бит^Зтб относительно небольшое количество информации; если с помощью двоичных символов нужно передавать более пространные сообщения, следует объединять вместе несколько знаков-из двоичных символов нужно составлять слова. Алфавит, из которого составляются такие слова, состоит из «букв» 0 и 1. Длина слов, т.е. число двоичных знаков, используемых на одно слово, есть прямая мера (в битах) количества информации, передаваемой в одном слове. Словом, состоящим из двух двоичных знаков, можно передать два бита, из трех-три и т.д. Число различных слов, которые могут быть составлены из двух двоичных знаков, равно 22 = 4. Это 00, 01, 10 и 11. С помощью трех знаков можно составить 23 = 8 слов следующего вида: 000, 001, 010, 011, 100, 101, ПО, 111. Очевидно, что используя т двоичных знаков на слово, можно составить п = 2т различных сообщений; процесс, конкретизирующий любое из них, передает т бит информации.
Обсуждавшееся до сих пор определение количества информации можно также применить и к случаям, в которых в качестве носителей информации служат любые произвольные символы. Любой желаемый набор символов можно представить двоичными последовательностями достаточной длины. Чтобы кодировать символы таким образом, т.е. чтобы получить однозначное соответствие между набором из п символов и двоичными словами, длина последних должна составлять в среднем т = log2 и двоичных знаков.
Принцип такого кодирования представлен на рис. 2-18. Это дерево выбора решений, в котором в результате последовательного раздвоения ветвей получается в точности по одной ветви на каждый символ (здесь нужно было представить 8 букв от А до Я). Каждое раздвоение символизирует выбор из двух возможностей. Если выбор левой ветви мы обозначим цифрой 0, а правой 1, то мы сможем построить соответствующие двоичные кодовые слова путем простого прохождения от «ствола» дерева к символам на конечных веточках. Получившиеся двоичные слова написаны под буквами, к которым они относятся.
Если такое кодовое дерево, или дерево выбора, строить для всего английского алфавита, то число выборов (точек раздвоения) будет равно первому целому числу, превышающему log2 26, или 5, так как 25 = = 32. Шесть двоичных слов, не понадобившихся для букв, можно использовать для кодирования знаков препинания и интервалов.
Но если произвольный знак можно заменить двоичным словом, то можно также сказать, что он содержит столько же информации (в битах), сколько и двоичное слово, которым он закодирован. Следовательно, среднее содержание информации I в акте определения одного символа из набора в п символов равно I = log2 п. Это [2-7], которое мы получили выше при определении количества информации.
Настоящее введение в основные концепции теории информации

Рис. 2-18. Кодовое дерево, или дерево выбора. Путем последовательных выборов из двух возможностей буквам от А до Н можно присвоить разные коды. В каждой точке раздвоения повороту влево ставится в соответствие знак 0, а повороту вправо-знак 1. Если начать с исходной точки и последовательно зафиксировать все знаки вдоль какой-то траектории, получится запись в двоичной системе той буквы, которая стоит у конечной точки (от А до Н). Эти двоичные слова приведены под соответствующими буквами.
сильно упрощено, в частности по причине допущения равной вероятности всех символов в наборе. Ссылки на более фундаментальные изложения теории информации приведены в конце книги.
Теория информации в сенсорной физиологии.Теперь мы применим идею, описанную выше в общих терминах, к передаче информации в нервной системе. Подходящим для обсуждения примером является рецептор с афферентным нервным волокном. Здесь информация кодируется и передается дальше в виде нервных импульсов. источниками информации служат раздражители окружающей среды, передатчиком - рёцеп-торная клетка, каналом передачи-нервное волокно, приемником - синапс некоторого центрального нейрона, а сам этот нейрон может рассматриваться как потребитель.
Физически измеримые параметры стимулов (например, интенсивность давления на кожу, положение стимула на периферической сенсорной поверхности, длины волн светового и звукового стимулов)-это передаваемые величины. На примере рецептора растяжения (разд. 2.1) мы видели, как параметры стимула определяют реакцию рецептора: частота импульсного разряда в афферентном волокне меняется в ту же сторону, что и интенсивность стимула. В этом случае переменная «интенсивность стимула» кодируется переменной «средняя частота нервных импульсов». Такой способ кодирования, сопоставимый с частотной модуляцией в технических системах связи, обнаружен в рецепторах всех модальностей: в мышечных веретенах, в кожных рецепторах давления, в хеморецепторах языка и фоторецепторах сетчатки носителем информации является частота нервных импульсов.
Поскольку афферентные волокна определенных рецепторов связаны с определенными клетками ЦНС, информация, содержащаяся в потоке импульсов, расшифровывается соответствующим образом. Например,
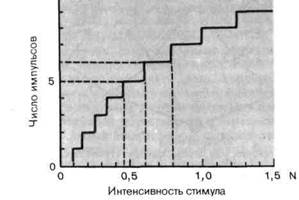
Рис. 2-19. Кодирование интенсивности стимула (абсцисса) нервными импульсами (ордината). Длительность каждого стимула фиксирована. В качестве примера взят механорецептор, подвергаемый действию силы (измеряемой в ньютонах). Характеристическая кривая процесса кодирования имеет форму лестницы (красная линия).
афференты 1а оканчиваются на гомонимных мотонейронах, а механо-чувствительные кожные афференты проецируются в постцентральную извилину.
Передача информации идеальным рецептором.Каким образом мы можем различить по сериям импульсов, посылаемых рецептором, те состояния, которые позволят описать содержащуюся информацию? Рассмотрим сначала кодирование интенсивности стимула. Если на определенном отрезке времени стимулируемый рецептор либо не выдает импульсов, либо генерирует один импульс, то он может обеспечить передачу информации только о двух уровнях интенсивности стимула. В этом случае отсутствие потенциалов действия означает, что «интенсивность стимула ниже порога», а один потенциал действия-что «интенсивность стимула выше порога». Если возможное число импульсов составляет 0, 1 и 2, то элемент-потребитель в такой системе получит информацию, достаточную для различения трех уровней стимуляции. Если стимул может возбуждать в афферентном волокне до N импульсов, то рецептор теоретически может сигнализировать в ЦНС об N + 1 уровнях интенсивности. Иллюстрация к такой ситуации дана на рис. 2-19. Число импульсов N в афферентном волокне (ордината) может принимать только целые значения. По этой причине кривая, соотносящая интенсивность стимула (абсцисса) с числом импульсов, имеет форму лестницы. У идеального рецептора, который реагирует на неизменный стимул постоянной частотой разряда, число импульсов N равно произведению частоты разряда / на время наблюдения V. N=f-t. Значит, максимальное число уровней интенсивности стимула, различимых по
активности одного нервного волокна, равно
N + 1=₤m t+1, [2-8]
где fm-максимальная частота разряда рецептора. В случае рецептора со спонтанной частотой разряда f0 (в отсутствие какого бы то ни было об-наружимого внешнего стимула) в [2-8] и во всех последующих выражениях fm следует заменить на fm —f0.
Таким образом, в данном случае число имеющихся в наличии символов-это число различимых состояний активности афферентного волокна. Следовательно, количество информации об интенсивности стимула в примере рис. 2-19 равно I = log2(N+ l) = log2 10= 3,3 бита. В общем случае для идеального рецептора, у которого частота разряда определяется стимулом, содержание в этом разряде информации относительно интенсивности стимула вычисляется по формуле
/ = log2(fm t+l). [2-9]
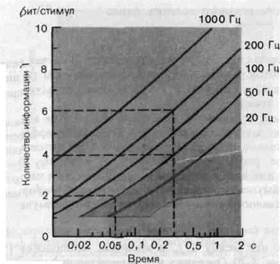
Это соотношение между /, fm и временем наблюдения t показано графически на рис. 2-20. Очевидно, что количество информации / возрастает как с увеличением fm, так и с увеличением t. Максимальная частота fm - фиксированное свойство рецептора. Вместе с тем, удлиняя время наблюдения t, теоретически можно получить сколь угодно точную информацию об интенсивности неизменного длительного стимула. Однако на практике свойства реальных рецепторов и динамика процесса декодирования в ЦНС ограничивают время, до которого можно растягивать интеграл оценки афферентного разряда в целях увеличения количества информации. Изучая реальные рецепторы, мы можем получить некоторое представление о пределе, до которого имеет смысл увеличивать г.
Передача информации реальным рецептором.На стимул постоянной интенсивности идеальный рецептор реагирует совершенно регулярным разрядом с неизменной частотой. В случае биологических рецепторов это условие не выполняется.
Экспериментально обнаружено, что при поддерживании постоянной интенсивности стимула частота разряда рецептора может меняться со временем. На рис. 2-21, А показан разряд рецептора давления кошачьей лапы для разных интенсивностей стимуляции. Бросается в глаза, что частота разряда-носитель информации об интенсивности стимула-флуктуирует стохастически (т. е. случайным образом, без видимой причины). Такие флуктуации сигналов в технике связи называют шумом. Они снижают качество работы информационного канала - вносят искажения в передачу информации (см. рис. 2-17).
Чтобы количественно оценить потери информации из-за шума в рецепторе, рассмотрим экспериментально полученное кодовое соотношение, приведенное на рис. 2-21, Б. каждая точка графика представляeт результат одного измерения, подобного показанному в части А, только
|

|
Рис 2-20 За8ИСИМОСТЬ содержания информации / (ордината) в реакциях идеального рецептсра от времени наблюдения t (абсцисса). Различные кривые соответствуют разл)1ЧНЫМ значениям максимальной частоты импульсов fm в разряде рецептора' кривые были вычислены на основании [2-9]. Красным отмечена область' в к0ТОРУю попадают соответствующие значения количества информации в реакц!1ЯХ механорецепторов кожи при изменении времени наблюдения t.
здесь врем? наблюдения равно 5 с. Число различимых состояний можно оценить построив на этой полосе точек ступенчатую кривую; та, что изображена здесь, оказалась имеющей восемь ступенек (первая располагается на уровне 0 импульсов), что соответствует 3 битам на стимул, если далее сгоит идеальный приемник, считающий в течение 5 с.
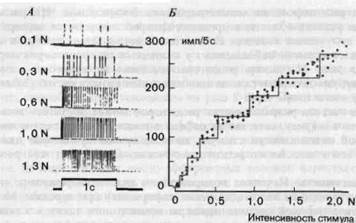
Рис. 2-21. Влияние шума на кодирование в рецепторе. А. Реальные записи разряда рецепторов давления в подошве лапы кошки в ответ на стимулы, действующие в течение 1 с; интенсивности стимулов указаны рядом с записями. Б. Значения частоты импульсов в реакциях на стимулы длительностью 5 с (ордината), полученные на основании многих записей типа А для стимулов разной интенсивности (абсцисса). Ступенчатая кривая (красная линия) построена таким образом, чтобы она вписывалась в полосу разброса данных, имея при этом ступеньки максимальной возможной высоты.
Основание для построения лестницы, изображенной на рис. 2-21, Б, следующее. Две интенсивности стимула четко различаются, если все значения числа импульсов (ордината на рис. 2-21, Б), соответствующие одной интенсивности, отличаются от значений, соответствующих другой интенсивности. «Наихудший случай», который представляет минимально возможное различение, задается ступенчатой кривой с максимальной высотой ступенек, которая может быть вписана в полосу точек кодового графика для экспериментально измеренных реакций.
Если бы данный рецептор мог работать как идеальный модулятор частоты (идеальный рецептор без шума), то в экспериментальных условиях рис. 2-21, £ можно было бы различить по крайней мере 300 градаций интенсивности стимула; соответствующее содержание информации составляло бы 8,2 бита на реакцию [2-9]. Следовательно, в этом примере на каждой реакции 8,2 — 3 = 5,2 бита теряется из-за шума!
Наивысшие значения количества информации на стимул, измеренные до сего времени, были обнаружены у деэфферентированных мышечных веретен. Первичные__окончания (Ia) могут передавать по 4,8 бита на 1 стимул; вторичные окончания (II) реально передают по 6,3 бита.
Отклонения функции реального рецептора от идеального также становятся очевидными, когда варьируют время наблюдения t. При удлинении t количество информации, передаваемой идеальным рецептором, монотонно растет, как это показано на рис. 2-20 кривыми, соответствующими [2-9]. Однако количество информации, передаваемой ре-

 альным рецептором, не может нарастать беспредельно. На рис. 2-20 красным указана область, в пределах которой изменяются экспериментально полученные значения количества информации на стимул в зависимости от времени наблюдения t у кожных механорецепторов определенного типа. Например, рецепторы давления на кошачьей лапе, по существу, уже достигают своих максимальных возможностей (3 бита на стимул) всего лишь через 1 с.
альным рецептором, не может нарастать беспредельно. На рис. 2-20 красным указана область, в пределах которой изменяются экспериментально полученные значения количества информации на стимул в зависимости от времени наблюдения t у кожных механорецепторов определенного типа. Например, рецепторы давления на кошачьей лапе, по существу, уже достигают своих максимальных возможностей (3 бита на стимул) всего лишь через 1 с.
Хотя частота разряда многих рецепторов может достигать нескольких сотен в секунду, качество их работы с точки зрения передачи информации об интенсивности стимула явно немногим лучше или даже не лучше, чем у идеального рецептора с максимальной частотой разряда 20 с‾1.
Избыточность.Неточное кодирование в реальном рецепторе (из-за шума)-это один из видов искажения информации при передаче. Можно ли найти в нервной системе примеры компенсации таких искажений? Методы, разработанные для предотвращения потерь информации в технике связи, используют введение избыточности. Чтобы пояснить это понятие, рассмотрим сначала пример из области лингвистики. Попробуйте расшифровать следующую последовательность букв:
Код.р.в...е в р.цеп...ах ис.аж... и.-з. ш.ма
Информацию, содержащуюся в этом предложении, можно восстановить, хотя около 40% букв отсутствует; письменный текст содержит больше символов, чем это необходимо для точного понимания его смысла; этот излишек и есть избыточность. Она измеряется в битах.
Исследования текстов, из которых систематическим образом изымались отдельные части, показали, что, например, письменный немецкий содержит в среднем лишь по 1,3 бита на букву. Теоретически среднее содержание информации в каждой из 26 букв алфавита равно log2 26 = = 4,7 бита, так что средняя избыточность в этом случае составляет 4,7 — 1,3 = 3,4 бита на букву.
С первого взгляда это может показаться расточительной тратой символов, но это только одна сторона избыточности. Ее достоинства становятся очевидными, когда в канале передачи возможны искажения -например, при плохой телефонной связи, радиоприеме в условиях помех или в случае неразборчивого почерка. Здесь избыточность языка обеспечивает узнавание текста, когда удается идентифицировать всего лишь часть знаков. В теории информации показано в общем виде, что передача информации тем надежнее застрахована от искажений, чем больше избыточность, введенная при кодировании.
Избыточность в нервной системе.Один из эффективных способов использования избыточности для защиты от шума состоит в передаче информации по двум или более каналам параллельно. Такая возможность реализуется в нервной системе. На периферии плотность рецепторов обычно так высока, что даже точечные стимулы возбуждают несколько
волокон. При такой параллельной передаче степень фактического использования периферической информации зависит от характера ее обработки в центральной нервной системе. В предположении, что оценка включает суммирование импульсов во всех возбужденных волокнах, получаемую наблюдателем информацию об интенсивности стимула можно вычислить на основании вариабельности суммарного разряда-например, способом, представленным на рис. 2-21, Б. При таком процессе суммации общее число импульсов в интервале наблюдения растет с увеличением числа активированных афферентных волокон приблизительно линейно. Вариабельность разряда (шум), т.е. ширина полосы неопределенности на рис. 2-21, Б, увеличивается в меньшей степени. В связи с этим, по мере того как число афферентных волокон нарастает, число шагов, которые могут быть изображены на экспериментально полученном кодовом графике (типа показанного на рис. 2-21, Б), увеличивается. Отсюда следует, что в суммарном разряде содержится больше информации, чем в разряде отдельного рецептора. Таким образом, обобщая, можно сказать, что избыточность, создаваемая передачей по параллельным каналам, компенсирует искажения, возникающие при кодировании в отдельном рецепторе.
Избыточность, создаваемая параллельной передачей информации, используется и внутри ЦНС. Но тут вступает в действие новый фактор: из-за конвергенции и дивергенции в сетях синаптических связей параллельные каналы могут действовать как весьма сложные цепи, которые (как показано в теории информации) могут в принципе обеспечить дополнительную избыточность.
Но если для сохранения информации об интенсивности стимула столь широко используется передача по параллельным каналам, то неизбежно должно наблюдаться обширное «растекание» возбуждения внутри ЦНС, о котором уже говорилось выше (см. рис. 2-8, А). Однако, как мы уже видели, такому растеканию может противодействовать латеральное торможение (см. рис. 2-8, Б). В зависимости от силы такого торможения в центральных представительствах периферии может подчеркиваться либо информация об интенсивности стимула, либо информация о его местоположении.
Информация в психологии. Вэкспериментальной психологии, и в особенности в психофизике (см. гл. 1), также используется количественное определение информации. Здесь мы приведем несколько примеров, подчеркивающих взаимосвязь между нейрофизиологическим и психофизическим измерением информации.
В процессе экспериментов люди могут субъективно оценивать интенсивность какого-нибудь стимула (например, яркость или давление на кожу) и выражать эти оценки каким-нибудь способом (например, численно, см. разд. 1.3). Если такие субъективные оценки изобразить точками против соответствующих значений интенсивности стимула, получится график типа изображенного на рис. 2-21, Б. На нем вместо числа импульсов, генерируемых рецептором (на ординате рис. 2-21, Б), мы те-
перь имеем численные выражения субъективной оценки интенсивности. Учитывая разброс данных, мы можем оценить соответствующее количество информации, имеющееся в наличии на уровне сознательного восприятия, с помощью уже описанной ступенчатой кривой. В экспериментах, связанных с субъективными оценками интенсивности давления на кожу, были получены значения порядка 3 бит/стимул; это примерно то же самое, что найдено для одиночного рецептора давления. Значит, в этом эксперименте для субъективных оценок интенсивности в восприятии достаточно информации, передаваемой отдельным нервным волокном, и, следовательно, вклад всех других возбужденных волокон -по крайней мере для этого очень частного психофизического вопроса об интенсивности стимула-может рассматриваться как избыточность.
В другом эксперименте испытуемого просили сравнивать два последовательных стимула и определять различия в их интенсивности. Сравнение количеств психофизической и рецепторной информации обнаружило, что, по крайней мере в случае психофизического различения Холодовых воздействий на кожу, в решение испытуемого вносит вклад информация, идущая по всем Холодовым волокнам стимулируемой области кожи (см. рис. 3-15), в этом случае вся имеющаяся в наличии нейронная информация используется для снижения дифференциального порога.
В заключение мы сравним общее количество сенсорной нейрофизиологической информации, которая может поступать в распоряжение субъекта, с соответствующим количеством психофизической информации. Для этого мы воспользуемся понятием максимального потока информации (бит/с); эту меру называют также емкостью (пропускной способностью) канала.
Емкость канала, например механорецептора (см. рис. 2-21), экспериментально определяется путем прогрессивного учащения последовательности стимулов при одновременном укорочении каждого из них. При снижении длительности стимула до значений менее 1 с содержание информации в реакции на отдельный стимул уменьшается (см. рис. 2-20), но из-за возрастания числа стимулов поток информации обычно возрастает. В табл. 2-2 суммированы данные о емкости каналов всех рецепторов в ряде органов чувств, полученные на основании общего числа афферентных волокон и емкости отдельных каналов. Они сравниваются с измерениями емкости психофизических каналов; это максимальный поток информации на уровне сознательного восприятия. В случае зрительной системы приводимое значение емкости относится к случаю чтения и определено в психофизических экспериментах. Для слуховой системы это емкость, связанная с пониманием речи.
Как мы знаем из нашего собственного опыта, в каждый данный момент времени мы можем полностью направить свое сознательное внимание только на одну сенсорную модальность. По этой причине маловероятно, чтобы человек мог одновременно обрабатывать более одного из тех максимальных психофизических потоков, которые приведены
Таблица 2-2.Сравнение потоков информации (емкости каналов) на уровне периферических нервов и сознательного восприятия. Слева указаны общее число рецепторов и афферентных волокон для пяти сенсорных систем и максимальный поток информации в каждой из них. Справа приведены данные по максимальным потокам информации на уровне сознательного восприятия-оценки емкости каналов, полученные в психофизических экспериментах
| Сенсорная система | Число рецепторов | Число афферентов | Общая емкость каналов, бит/с | Психофизическая оценка емкости каналов, бит/с |
| Зрительная | 2-Ю8 | 2-106 | ю7 | |
| Слуховая | 3-Ю4 | 2 10* | ю5 | |
| Тактильная | 107 | 106 | 106 | |
| Вкусовая | 3-Ю7 | 103 | 103 | 1 (?) |
| Обонятельная | 7-Ю7 | 105 | 105 | 1 (?) |
в табл. 2-2 справа. Следовательно, мы можем заключить, что максимальный поток информации в процессе сознательного сенсорного восприятия составляет около 40 бит/с-т. е. на много порядков ниже, чем передаваемый рецепторами (левая часть табл. 2-2). Таким образом, получается, что наше восприятие, по-видимому, ограничивается ничтожной частью всего обилия информации, имеющейся в наличии на сенсорных входах.
В 2.20. Для случая кодирования рецептором интенсивности стимула количество информации может быть определено
а) как число различимых значений частоты разряда рецептора;
б) как число потенциалов действия, генерируемых в единицу
времени;
в) как логарифм по основанию 2 числа уровней интенсивности стимула, различаемых по разряду рецептора;
г) только в том случае, если отсутствуют статистические флуктуации частоты разряда (нет шума)
. В 2.21. Какие из следующих утверждений относительно избыточности верны?
а) Избыточность в принципе связана с увеличением мощности, затрачиваемой на передачу информации, по сравнению и необходимым минимумом,
б) Избыточность-это увеличение количества нформации, передаваемой по нервному волокну, за счет укорочения рефрактерного периода.
в) Избыточность реализуется в нервной системе путем передачи одной и той же информации по нескольким параллельным каналам,
г) Как правило, подверженность информации искажениям увеличивается с увеличением избыточности.
 22. Следующие утверждения применимы к понятию «количество информации».
22. Следующие утверждения применимы к понятию «количество информации».
а) Словам английского языка нельзя приписать никаких значе
ний количества информации, поскольку эти слова имеют
смысл, который нельзя измерить (семантическая информа
ция).
б) Количество информации в каждом отдельном броске играль
ной кости с шестью гранями равно I = log10 (6) бит.
в) Когда произвольный символ кодируется двоичными знаками,
количество информации в нем всегда неизбежно становится
меньше (потеря информации).
г) Количество информации в акте выбора некоторого символа зависит от вероятности его появления.
Дата добавления: 2015-10-05; просмотров: 1126;
