Практические задания.

1. Автомат случайно с одинаковыми вероятностями генерирует трехзначные десятичные числа, у которых первая цифра выбирается из набора {7,8,9}, вторая независимо – из набора {4,5,6},третья независимо – из набора {0,1,2,3,7,8,9}. Найти вероятности появления каждого из таких чисел.

2. На цветовом табло 3 различных позиции. В каждой из них можно использовать один из цветов: красный, синий, зеленый или желтый. Сколько существует различных вариантов заполнения табло при условиях:

а) цвета могут повторяться в различных позициях,

б) цвета в различных позициях должны обязательно различаться.

3. Сколько существует всего трехзначных целых чисел в системе счисления с основанием 7, у которых в записях присутствуют только нечетные цифры?

4. Красный, зеленый и синий кубики случайно расставляют на пронумерованных клетках квадратной доски размером 3´3. На одной клетке может быть помещено не более 1 кубика. Какова вероятность выпадения каждого варианта расстановки, если все они равновероятны? Ответ дать формулой.

5. Сколькими способами можно разместить 5 шаров в 8 различных лунках при условии, что 1) все шары одинаковы; 2) все шары различны?

6. На 8различных местах располагают 3 одинаковых кубика и 5 одинаковых шариков. Сколько существует различных вариантов их расположения?

7. Целочисленная величина принимает четные значения в 3 раза чаще, чем нечетные. Определить вероятность выпадения четных величин и вероятность выпадения нечетных величин.

8. Найти максимальное число мест n, при котором общее число вариантов расположения на них 4 одинаковых объектов не превышает 1000.

9. Найти максимальное число мест n, при котором число вариантов расположения на них (n – 2) различных одинаковых объектов менее 600.

10. Рассчитать максимальное число попарно различных объектов, размещаемых на 4 различных местах не более чем 1300 различными способами.

11. В 2n пронумерованных проточках кольцевой детали устанавливают поочередно детали типов А и В. Число деталей А равно n, деталей B – также n. Найти общее число вариантов их размещения, если детали А попарно различны, а детали типа В одинаковы.

12. Решить задачу 11 в предположении, что все детали В также попарно различны.

13. Сколько различных слов (в том числе – не имеющих смысла) можно получить путем всех возможных перестановок букв в слове «комбинаторика»?

14. Алгоритм обрабатывает пары множеств (порядок в паре не имеет значения) из набора, содержащего 3 одинаковых и 5 попарно различных множеств. Найти общее количество различных способов выбора пар множеств.

15. Множество содержит 4 одинаковых объекта и 4 различных. Сколько существует всех возможных вариантов выборок из данного множества по 6 объектов? Порядок вхождения объектов в выборку не имеет значения.

16. В цехе необходимо расставить 7 новых станков, их которых
3 одинаковы, остальные – различны. Найти общее количество различных вариантов их расстановки на выделенных для этого 8 различных местах.

17. В спортивном состязании присуждается одно первое место, одно второе и два третьих (порядок третьих призеров не имеет различия). Найти общее число вариантов ранжирования призеров при 10 участниках.

18. Сколько существует различных шестизначных чисел в десятичной системе счисления, у которых в записи:

а) ровно две одинаковых цифры,

б) ровно три одинаковых цифры,

в) не менее четырех одинаковых цифр,

г) не более трех одинаковых цифр?

Ответы дать в виде формул.

19. Рассмотрим множество всех полных перестановок {p (1, 2, …
... , n ) }, имеющих равные вероятности. Доказать, что:

а) средневероятный вес вектора инверсий перестановок
w _и (d) равен n(n-1)/4;

б) количество всех подстановок, у которых в векторах инверсии встречаются только числа от 0до k включительно, равно
N _k = (k+1)^n-k-1(k+1)!;

в) общее число нулей в векторах инверсий всех полных перестановок длины n равно n!(1 + 1/2 + 1/3 + ... + 1/n);

г) вероятность того, что максимальная компонента вектора инверсий перестановки равна k, выражается числом

р_k = [(k+1)^n-k-1(k+1)! – k ^n-k k!].

7. Доказать, что:

а) число всевозможных частичных перестановок длины k, имеющих ровно один нуль в векторе инверсий, равно ;

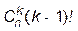б) число всевозможных частичных перестановок 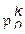длины k, имеющих ровно k – 1 нулей в векторе инверсий, равно

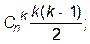
в) общее число нулей в векторах инверсий всех частичных перестановок длины k {p^k_n} равно

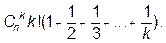
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ТЕМЕ