Сочетания. Сочетаниями из n по k называют расположения k одинаковых объектов на n различных местах, когда на одно место можно поместить только один объект

Сочетаниями из n по k называют расположения k одинаковых объектов на n различных местах, когда на одно место можно поместить только один объект. Общее количество N(C(А)) всех таких возможных попарно различных сочетаний обозначают как C(n, k) либо .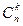

Поскольку сочетание из n по k можно представить как частный случай размещения без повторений одной группы одинаковых объектов (s = 1, k = s), то расчет общего числа сочетаний выполняют по формуле

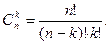
Расчетная формула 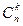для сочетаний из n по k выводится из формулы для размещений без повторения с использованием правила учета сходства–различия. Используя в качестве промежуточной формулу 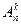для размещений без повторений и обратную схему (рис. 5.6) для правила учета сходства-различия, получим схему на рис. 5.9:

Рис. 5.9. Расчетная схема для расчета числа 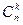сочетаний из n по k

Замечание. Все формулы для подсчета чисел основных случаев расположения k объектов в п. 5.3–5.6 выведены при условии, что все n мест, отведенных для размещения объектов, различны. Однако если это условие не выполняется и все n мест одинаковы, то для фиксированного набора объектов при k £ n число мест не имеет значения и вариант размещения данного набора только один.

Например, необходимо подсчитать яблоки. Для этого их в произвольном порядке высыпают на стол. С точки зрения решаемой задачи не важно, в какое место стола, какое яблоко попадает, важны лишь свойства размещаемого набора – в данном случае количественные. Для задачи подсчета яблок вариант их расположения на столе один.

Пример 1.Найти, сколькими вариантами можно разместить 4 одинаковых шара на 7 местах в случаях, когда: 1) все места различны; 2) все места неразличимы между собой.

Решение. В случае 1) получаем подсчета общего числа сочетаний для 4 одинаковых шаров на 7 различных местах:

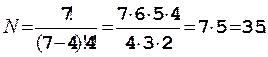
В случае 2) все возможные варианты размещения одинаковы, поэтому N = 1.

Ответ: 1) 35; 2) 1.