Перестановки и размещения без повторений различных объектов. Упорядоченность перестановок

Перестановкой длины n называют расположение n различных объектов на n различных местах. Общее количество N(C(А)) всех возможных попарно различных перестановок длины n обозначают как P(n), A(n, n) либо .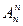

Размещением без повторений из n по k (n ³ k) называют расположение k взаимно различных объектов на n различных местах (не более одного объекта на место). Общее количество мест не меньше числа объектов. Полное количество N(C(А)) всех различных вариантов размещений без повторений из k по n обозначают как A (k, n) либо 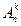. Очевидно, что перестановки – частный случай размещений без повторений при равном количестве объектов и мест, т. е. k = n.

Подсчет общего числа вариантов расположения объектов в этом случае проще всего производить при помощи чисел вариантов N(a₁), N(a₂), …, N(a_k) расположения каждого из объектов 1,2, ..., k.

Первый из размещаемых объектов можно разместить на любом из n имеющихся мест (число вариантов выбора N(a₁) = n). Для второго размещаемого объекта число вариантов выбора N(a₂) = n – 1, поскольку одно место уже занято. Для третьего по порядку размещаемого объекта
N(a₃) = n – 3, т. д., для k-го – N(a_k) = (n – k + 1).

По правилу умножения общее количество вариантов размещений без повторений из n по k равно произведению чисел вариантов N(a₁), N(a₂), ×××, N(a_k):

.

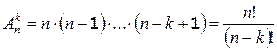Вывод расчетной формулы для общего числа вариантов размещений без повторений k различных объектов на n местах с использованием правила умножения поясняется схемой на рис. 5.8.

Рис. 5.8. Расчетная схема для подсчета общего числа вариантов 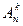размещений без повторений k различных объектов на n местах

Общее число перестановок длины n:

.

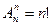Пример 1.Определить, сколькими вариантами можно разместить четырех гостей за столом, если число стульев, занимающих различные положения (различающихся), равно: 1) 4; 2) 6?

Решение. В случае 1) имеет место расчет перестановок, так как количество объектов равно числу мест для размещения: k = n. Поэтому

.

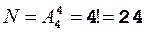В случае 2) число мест для размещения больше, чем число объектов (n > k), поэтому необходимо использовать формулу для расчета размещений без повторений из 6 по 4:

.

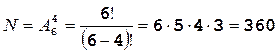Ответ: 1) 24; 2) 360.

Замечание. Обычно при расчете размещений без повторений полагают, что мест n не меньше, чем объектов k (n ³ k). Однако на практике количество объектов k может быть больше, чем мест для размещения n (k > n). Данный случай можно рассматривать аналогично предыдущему, представив его как распределение n мест по k объектам. При этом количество возможных размещений равно k! / (k – n)!.

Таким образом, в задаче о распределении k неодинаковых объектов на n различных местах количество возможных размещений всегда можно представить в виде общей формулы:

,
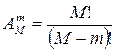где M = max(k, n); m = min(k, n).

Пример 2.Найти число вариантов размещения на 6 пронумерованных рабочих позициях станка различных инструментов, общее число которых равно 8.

Решение. Так как места и инструменты различны и k = 8 > n = 6, то M = max(k, n) = 8; m = min(k, n) = 6. Общее число вариантов размещения:

.

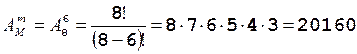Ответ: 20160.

При подсчете вариантов вместо n неодинаковых объектов всегда можно взять n различных натуральных чисел, например,
1, 2, ..., n.

Определение. Полной перестановкой p_n (1, 2, ..., n) называют результат перестановки длины n чисел 1, 2, ..., n, куда каждое из них входит лишь раз. Общее количество перестановок {p_n}равно 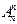= n!. Частичной перестановкой длины k p^k_n (1, 2, ..., n) будем называть результат размещениями без повторений k различных чисел из {1, 2, ..., n}. Общее количество перестановок {p^k_n}равно 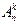= n!/(n-k)!.

Пару элементов в перестановке (а_i, а_j) будем считать упорядоченной, если а_i < а_j при i < j. Каждую полную перестановку чисел p (1, 2,..., n) =(p₁, p₂, ...,p_n) можно взаимно однозначно охарактеризовать вектором инверсий `d = (d<sub>1</sub>, d<sub>2</sub>, ..., d<sub>n</sub>), определяющим меру неупорядоченности перестановки p. Это соответствие устанавливают следующим образом: каждый элемент d<sub>i</sub> равен числу элементов, стоящих слева от p<sub>i</sub> и превышающих его (т. е. нарушающих порядок). У первого элемента d<sub>1</sub>= 0. Полностью упорядоченной перестановке чисел (1, 2, ..., n) соответствует `d_min = (0, 0, ..., 0), а максимально неупорядоченной перестановке (n, n–1, ..., 1) — вектор инверсий d_max =(0, 1,…, n–2, n–1). Каждый вектор инверсий можно рассматривать как обращенную слева – направо запись некоторого числа N(d) в факториальной системе счисления. Вектору N (d_min) соответствует 0, вектору N( 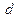_max) — число (n!–1). Следовательно, множество всех полных перестановок p(1, 2, ..., n)можно взаимно однозначно отобразить на множество всех целых чисел от 0до (n! –1).

Определение. Весом вектора инверсий `d = (d₁, d₂, ..., d_n) называют сумму его компонент:

w _и (`d ) = d₁ + d₂ + ... + d_n .

Вес вектора инверсийперестановки p = (p₁, p₂, ..., p_n) равен количеству перемен мест рядом стоящих элементов, необходимому для полного упорядочения перестановки, соответствующей вектору `d.