Размещения (размещения с повторениями)

Изучим основные типовые случаи расчета общего числа вариантов расположений объектов на выделенных местах.

Рассмотрим n мест a₁, a₂,…, a_n, для которых порядок расположения имеет значение и на которых могут независимо расположены представители из одного и того же множества, имеющего m объектов, при этом располагаемые объекты на разных местах могут иметь одинаковые значения (повторяться). Например, разряды десятичного числа, вносящие в него различный вклад, могут независимо принимать m = 10 значений от 0 до 9.

Данный способ расположения объектов называют размещением из n по m. Общее количество N(C(А)) вариантов всех рассматриваемых комбинаторных множеств C(А) обозначают U(n, m) либо 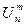. Поскольку значения величин могут неограниченное число раз повторяться при размещении на различных местах, то данный случай также можно назвать размещением с повторениями.

Поскольку для каждого места a₁, a₂, …, a_n число вариантов возможного расположения объектов не зависит от остальных и равно m, то, применяя (n-1) раз правило умножения, получим общую формулу для расчета :

.

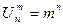Вывод расчетной формулы для общего числа вариантов 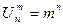размещений с повторениями m различных объектов на n местах с использованием правила умножения поясняется на схеме на рис. 5.7.

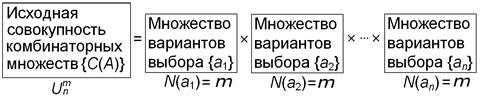
Рис. 5.7. Расчетная схема для подсчета общего числа вариантов размещений с повторениями m различных объектов на n местах

Многие практические задачи оценки количества объектов сводятся к подсчету размещений.

Пример 1.Найти количество N попарно различных трехзначных десятичных чисел для двух случаев:

1) когда в начале записей разрешены незначащие нули;

2) когда в записях незначащие нули недопустимы.

Решение.

1) Если нет ограничения на использование нулей, то в каждом разряде чисел может быть до 10цифр: 0,1,2,3,4,5,6,7,8,9. Получаем задачу размещения со следующими параметрами: n = 3, k = 10. Следовательно:

.

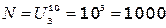2) Если использование незначащих нулей в начале записи чисел недопустимо, то в каждом из двух младших разрядов, как и в случае 1), может быть одна из 10 цифр, а в старшем разряде только одна из 9 цифр: (1,2,3,4,5,6,7,8,9). Поскольку цифры в разрядах независимы, то общее количество различных чисел в данном случае по правилу умножения составит:

N = 9×10² = 900.

Ответ: 1) 1000; 2) 900.