Уравнения тепломассопереноса

Пусть мы имеем дело с каким-либо скалярным полем, например, полем температур: T = f (х, у, z, t),(7.13)

где х, у, z — координаты точки пространства; t - время.

Если температура Т меняется во времени, то температурное поле называют неустановившимся или нестационарным. В противном случае его называют стационарным или установившимся.

Рассмотрим в трехмерном пространстве две изотермические поверхности, все точки которых имеют температуры Т- для пер­вой поверхности и Т + 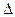Т для второй. Так как в одной и той же точке пространства не может быть двух разных температур, то такие поверхности не пересекаются. Изменение температур в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности. Наиболее резкое изменение температуры оказывается в направлении нормали nк изотермической поверх­ности. Вектор, длина которого равна пределу отношения изменения температуры 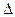Т к расстоянию 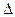n между изотермическими поверхностями по нормали, а направление совпадает с направлением нормали, называют температурным градиентом:

lim 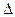T/ n = dT/dn = \gradT\ ,K/м;(7.14)

Таким образом, grad T - вектор, направленный по нормали к поверхпости уровня в сторону возрастания Т и численно равный скорости изменения Т по направлению. Для скалярного поля Т (х, у, z) вектор вычисляют по формуле:

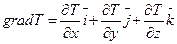(7.15)

где i, j, k - единичные векторы, направленные по координатным осям х, у и z. Аналогичные рассуждения справедливы и для поля концентраций.

Теперь перейдем к рассмотрению основных законов тепломассо-передачи.

1. Передачу тепла в неподвижной среде описывают законом Фурье

q = - 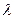grad T , Вт/м²(7.16)

гдеq - тепловой поток (количество тепла, переданое через единицу поверхности за единицу времени); 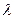-коэффициент теплопроводности, Вт/(м.К).

2. Аналогом закона Фурье для переноса вещества - является закон Фика:

j = -D grad C , кг/(м².с)(7.17)

где С - концентрация вещества; j - диффузионный поток; D - коэффициент диффузии, м²/с.

Эти законы применимы при соблюдении определенных условий:

1) законы относятся к молекулярному переносу в неподвижной среде;

2) закон Фурье в этой форме описывает перенос тепла в среде однородного химического состава;

3) закон Фика в рассматриваемой форме справедлив для изо­термических процессов и диффузии, независимой от диффузии других компонентов.

Процессы диффузии и теплопроводности в неподвижной среде можно наблюдать лишь в твердых телах. В газах и жидкостях на эти процессы неизбежно оказывает влияние движе­ние среды как целого - свободная и вынужденная конвекции. Если линейную скорость потока обозначить через w, то закон Фурье с учетом конвекции можно записать следующим образом:

q = - 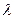grad T + c_p 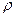w T,Вт/м² (7.18)

где c_p -теплоемкость при постоянном давлении, Дж/(кг.К); 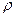- плотность, кг/м3; w - скорость, м/с.

Закон Фика примет следующий вид:

j = -D grad C + wC,кг/(м².с) (7.19)

Рассмотренные законы можно записать и в виде дифферен­циальных уравнений. 3акон Фика записывают, как

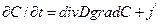(7.20)

где div- оператор дивергенции (если 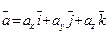, то );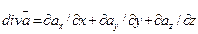

j’ - плотность источников вещества, т. е. количество веще­ства, образующегося вследствие химических реакций в единице объема в единицу времени.

При постоянном D можно записать

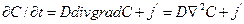(7.21)

где 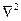- оператор Лапласа ( ).

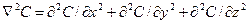Закон Фурье принимает следующий вид:

c_p 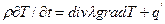,Вт/м²(7.22)

где q’ - плотность источников тепла, т. е. количество тепла, вы­деляющегося вследствие химических реакций в единице объема в единицу времени. Если 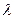считать постоянным, то: 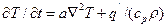(7.23)

где 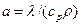- коэффициент температуропроводности, м²/ч.

При наличии конвекции в уравнения законов Фика и Фурье следует добавить соответственно w grad Cи w grad Т, где w - ско­рость потока.

В некоторых случаях дифференциальные уравнения диффузии и теплопередач при использовании соответствующйх граничных и начальных условий могут быть решены. Если речь идет о пере­носе тепла и вещества в условиях конвекции, то уравнения нужно решать совместно с уравнениями гидродинамики.

Процесс передачи тепла и вещества при конвективном движе­нии, особенно когда движение носит турбулентный характер, не всегда поддается аналитическому расчету. Поэтому в таких слу­чаях прибегают к эмпирическим законам.

Тепловой поток в виде выражения называемого законом Ньютона:

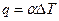;Вт/м2,(7.24)

где 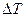— разность температур, К; 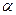-коэффициент теплоотдачи, Вт/(м².К).

Для расчета процесса переноса вещества пользуются выражением:

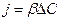; кг/м².c (7.25)

где j - диффузионный поток; 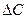- разность концентраций, кг/м³; 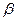- коэффициент массопередачи, м/с.

С точки зрения размерности величина 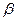соответ­ствует не коэффициенту теплоотдачи а, а его отношению к тепло­емкости единицы объема .

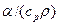Сущест­вует вид передачи тепла независимо от окружающей среды - теп­ловым излучением. Теплообмен между двумя поверхностями, нагретыми до темпе­ратур Т₁ и Т₂ согласно закону Стефана - Больцмана, равен

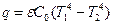; Вт/м2, (7.26)

где 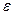- приведенная степень черноты системы; С₀ - коэффициент лучеиспускания абсолютно черного тела, Вт/(м².К⁴).

На практике передача тепла теплопроводностью, конвекцией и излучением часто происходит одновременно. В этом случае пользуются общим коэффициентом теплопере­дачи [17], записывая тепловой поток в виде

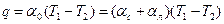;Вт/м2, (7.27)

где 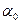- общий коэффициент теплоотдачи; 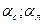- коэффициенты теплоотдачи соприкосновением и лучеиспусканием.

Иногда расчетное уравнение удобнее представить в форме, ана­логичной той, которая применяется для расчета лучистого тепло­обмена:

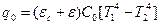; Вт/м2. (7.28)

Здесь конвективный теплообмен учитывают, увели­чивая приведенную степень черноты на некоторую величину .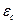

В модели включают уравнения, описывающие законы сохранения вещества и энергии, состояние среды и ее движение, равновесие, химическую реакцию, диффузию и др.

Контрольные вопросы:

1. Какими уравнениями можно описать металлургический процесс.

2. Вид уравнения мгновенного материального баланса.

3. Вид уравнения мгновенного теплового баланса.

4. Вид уравнения баланса импульса потока.

5. Сущность стационарного и нестационарного температурного поля, что называют температурным градиентом, тепловым потоком.

6. Для описания каких процессов используется закон Фурье и закон Фика.

7. Законы описания передачи тепла и вещества при конвективном движении.

8. Когда применяют закон Стефана—Больцмана.