Теория размерностей.

Число критериев можно умень­шить, используя векторную теорию размерностей. Дополнитель­ная размерность получается в результате введения векторных- ве­личин длины L_x, L_y, L_z. Пусть ось z совпадает с направлением действия гравитационной силы. Тогда, очевидно [w] = L_z T^-1 и [g] = L_z T^-2

Для такой характеристики, как плотность, все оси являются равноправными, поэтому

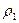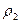[ ]=[ ] = L_x^-1 L_y^-1 L_z^-1M(8.4)

Очевидно также, что диаметр шара, параллельный направле­нию движения не влияет на скорость движения. В силу этого размерность эффективного диаметра должна быть представлена не величиной L_z, а комбинацией L_x и L_y. При записи комбина­ции нужно учитывать, что система симметрична отно­сительно оси z. Осевая симметрия требует равноправия размерно­стей L_x и L_y. Поэтому:

[d] = L_x^1/2 и L_y^1/2 ;(8.5)

Несколько более сложно обстоит дело с исключением асимме­тричности формулы размерности для вязкости. Вязкость - сила, действующая на единицу площади при единичном градиенте скорости. Поэтому один из видов формулы для вязкости таков:

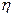[ _x] = [( сила/площадь)/градиент скорости]= [(L_zМТ^-2)/(L_y L_z)]/(L_zT^-1)/L_x] = L_x L_y^-1 L_z^-1M T^-1 (8.6)

Точно так же [ 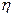_z] = L_x^-1 L_y L_z^-1M T^-1

В связи с необходимостью обязательно учитывать осевую сим­метрию в формулах размерности следует использовать выражение

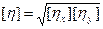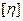т.е =L_z^-1M T^-1(8.7)

Теперь уравнение размерности можно записать следующим обра­зом:

L_z T^-1= (L_x^-1 L_y^-1 L_z^-1M)^a (L_x^1/2 L_y^1/2)^b (L_x^-1 L_y^-1 L_z^-1M)^c (L_z^-1M T^-1)^e(L_z T^-2)^f(8.8)

Здесь пять неизвестных показателей соответствуют пяти пер­вичным единицам намерения. Однако из-за условий осевой сим­метрии уравнения, которые соответствуют размерностям L_xиL_y , одинаковы. Остаются четыре уравнения, связывающие пять неиз­вестных. Решение этих уравнений дает

а = 1—с, b = 2, с = с, е = -1, f = 1.

Таким образом, мы получаем

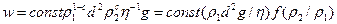(8.9)

Из механики известно, что

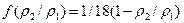(8.10)

Тогда

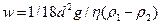(8.11)

Рассмотрим способы составления математической модели процесса, в которых используются критерии подобия. Иногда связь между критериями можно найти расчетным путем, решив соответствующую систему дифференциальных уравнений. Например, в рассмотренной выше задаче об охлаждении плиты решение отыскивается в виде функции

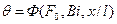(8.12)

Функция Ф найдена и представлена в литературе в виде номограмм,.

Если решить систему не представляется возможным, то связь между критериями находят экспериментальным путем. Например, изучали ско­рость слива шлака из конвертора. Рассматривались величины: G_ш - скорость слива шлака, м³/с; d - диаметр сливного отверстия (горловины), м; 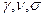- соответственно удельный вес (Н/м³); кинематическая вязкость (м²/с) и поверхностное натяжение жидкости (шлака), Н/м; g - ускорение свободного падения, м/с²; р - гидростатический напор, равный 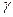_* h , Па (h - геоме­трический напор, м); С^* - безразмерная константа. Методами анализа размерностей найдено, что

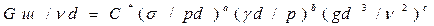(8.13)

В этом равенстве неизвестными являются G_ш, С*, а, b и с. Для их определения авторы измеряли скорость слива четырех различ­ных по свойствам жидкостей при соблюдении прочих равных усло­вий.

Иногда математическая модель процесса в принципе известна из теоретических соображений. Однако для нахождения числен­ных значений коэффициентов, входящих в эту модель, пользуются критериями подобия.

Контрольные вопросы:

1. Методы нахождения зави­симости между критериями подобия.

2. Применение теории подобия и полученных зависимостей, для описания аналогичных систем.

3. Способы нахождения с помощью анализа размерно­стей числа и вида безразмерных комплексов, используемых для описания различных явлений.

4. Что дает применение векторой теории размерностей.