Определение числа и видов критериев подобия.
Рассмотрим способы нахождения с помощью анализа размерностей числа и вида безразмерных комплексов, используемых для описания различных явлений. Процесс исследования начинают с выбора независимых переменных, оказывающих воздействие на систему. Здесь необходимо рассматривать также размерные коэффициенты и физические константы, если они играют важную роль в изучаемом процессе. Это наиболее важный этап всего исследования. После выбора переменных выбирают систему основных размерностей, через которую можно выразить единицы измерения всех рассматриваемых переменных.
Следующим этапом является подсчет числа названных выше безразмерных комплексов с помощью П-теоремы Букингема. Пусть число рассматриваемых переменных равно N. Пусть все они измерены в каких-то единицах. Эти единицы могут быть первичными (основа различных систем измерения - м, с, кг и т. п.) и вторичными (произведения первичных, взятых в различных степенях- м.с-1, м.с-2 и т. п.). Пусть число первичных единиц равно r. Согласно П-теореме число безразмерных величин равно (N - r) или меньше его.
Среди рассматриваемых переменных могут оказаться параметры одной и той же физической природы (линейные размеры, плотности и др.). Предположим, что n- число параметров разной физической природы среди изучаемых переменных. Тогда, кроме критериев-комплексов, вводятся в рассмотрение критерии-симплексы, и П-теорема формулируется следующим образом: число безразмерных критериев, определяющих рассматриваемое явление, К = N – r.
Из них число критериев-комплексов равно k = n-r, а число критериев-симплексов равно s = N-n.
Пример: М. П. Собакин и Я. Д. Вербицкий [56, с. 180-189] изучали барботаж газов через двухфазную ванну и при этом рассматривали следующие переменные и параметры: Н - среднюю глубину барботируемой ванны, м; Lм - глубину спокойной металлической ванны, м; d- диаметр ванны, м; w - средний расход газа, отнесенный к площади зеркала спокойной ванны, м/с;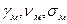 
- соответственно удельный вес (Н/м3), кинетическую вязкость (м2/с) металла и поверхностное натяжение (Н/м) на границе газ-металл; 
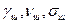- те же величины для шлака и для границы газ-шлак; g- ускорение свободного падения, м/с2; p - гидростатическое давление жидкости (шлака и металла) на дно ванны, Па.
Здесь число N размерных параметров равно 12. Из них n = 7 - число параметров разной физической природы. Эти параметры образованы первичными размерностями r = 3. В соответствии с П-теоремой общее число критериев должно быть равно:
К = N – r =12 – 3 = 9; (8.1)
в том числе критериев-комплексов k = n-r = 7 – 3 = 4 и критериев-симплексов s = N - n = 12 - 7 = 5.
В качестве переменных можно выбирать необязательно те переменные, которые кладутся в основу различных систем измерения. Например, в качестве таких переменных можно из рассматриваемой совокупности выбирать те, которые не образуют безразмерные комбинации.
Ван Дрист предложил модифицированную П- теорему, учитывающую такие случаи. Его метод формулируется следующим образом: «Число безразмерных комбинаций полной системы равно общему числу переменных минус максимальное число этих переменных, не образующих безразмерной комбинации». Однако во многих случаях это «максимальное число» не просто определить.
Из П-теоремы ясно, что иногда, применяя аппарат теории размерностей, можно с точностью до константы установить вид зависимости между рассматриваемыми переменными. Очевидно, должно выполняться равенство
N - r = 1(8.2)
Для нахождения вида комплексов (критериев подобия) наибольшее распространение получили следующие способы:
· использование принципа однородности размерностей;
· метод последовательного исключения размерностей (метод Ипсена);
· применение П-теоремы;
· использование системы дифференциальных уравнений.
Эти способы рассмотрены подробно в литературе [1 с. 89-99]. Для экспериментатора является естественным стремление свести исходный набор переменных к минимальному числу безразмерных комплексов. Здесь иногда может оказаться очень полезной векторная теория размерностей. Сущность метода, основанного на этой теории, заключается в следующем. Обычно три линейных размера по трем взаимо перпендикулярным осям имеют одну единицу измерения. Однако в реальных физических задачах геометрические размеры исследуемой системы неравнозначны. Исходя из этого, в векторной теории размерностей вводят три различные единицы измерения, соответствующие высоте, длине и ширине тела. Таким образом, число первичных единиц измерения увеличивается на две единицы, а количество критериев в соответствии с П-теоремой настолько же сокращается. Число первичных единиц можно также увеличить, введя дополнительно положительное и отрицательное значения длины.
Рассмотрим задачу Стокса о падении шара малых размеров под действием силы тяжести в вязкой среде. Предполагается, что падение такого шара не вызывает турбулентности. Размерности величин, фигурирующих в задаче, в системе LMT (анализ размерностей) записывают следующим образом: w- скорость шара, LT-1;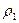 
- плотность шара, L-3М; d - диаметр шара, L; 
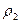- плотность среды, L-3М; 
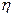- вязкость среды, L-1МТ-1; g - ускорение свободного падения, LT-2.
Здесь имеются шесть переменных и три первичных размерности. Следовательно, функция должна зависеть от трех критериев.
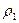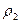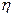f (w, , d, , , g) = 0(8.3)
Дата добавления: 2015-10-05; просмотров: 1095;