Проверка достоверности модели

Для обеспечения соответствия модели реальной системе приходится проделывать работу на всех этапах создания модели [27, с.213-224]. Еще до реализации модели возвращаются к постановке задачи, проверяют замысел модели, а также достоверность информации и источников. Повторно рассматривают критерий эффективности модели, аппроксимации реальных процессов, при­нятые допущения и гипотезы относительно механизма явления и другие аспекты.

В процессе реализации модели трижды проверяют ее досто­верность:

1. Первая проверка - после того, как создана логическая блок-схема модели и записаны ее основные уравнения. Выяс­няют, насколько логическая блок-схема и уравнения отражают замысел модели- смотрят, как каждая функция модели реализуется в блок-схеме, проверяя полноту схемы. Далее проверяют:

· правильность связей - нет ли в схеме непредвиденных связей и нелогичных ветвей;

· ясность и точность описания блоков, входные и выходные величины блоков и подбло­ков;

· все логические циклы, убеждаясь, что каждый из них имеет вход и выход;

· правильность уравнений, размерности всех вели­чин в уравнениях;

· правильность задания констант, работу дат­чиков случайных чисел и всех функций.

2. При второй проверке устанавливают соответствие между про­цессами, описываемыми программой и логической блок-схемой. Для этого сравнивают каждую операцию, представленную блок- схемой программы, с аналогичной ей операцией в логической блок-схеме.

3. Третья проверка - это проверка достоверности программы модели. Прежде всего, осуществляют обратный перевод программы в блок-схему и сопоставляют эту схему с имевшейся ранее. Затем проверяют отдельные части программы, решая на ЭВМ с их помощью задачи-тесты. После выполнения этой работы программу объединяют и проверяют модель в целом. Можно выделить три аспекта проблемы установления степени близости модели и объекта:

·Представление модели в виде логически упорядоченной после­довательности блоков, каждый из которых выполняет какую-либо элементарную операцию, позволяет считать модель истинной в том случае, когда признают истинными исходные данные и соблю­даются правила логического вывода (аналитическая истинность).

·Для моделей, реализуемых на ЭВМ, аналитическая истинность следует из того, что корректно составленная программа гаранти­рует адекватное функционирование моделирующего алгоритма.

·Правильность логического построения программы должна быть подтверждена ее содержательной интерпретацией.

Здесь имеют дело с концепцией семантической истинности, основным критерием которой служит гомоморфизм структур и организаций моделируемых систем, аналогичность функционирования моделей и объектов. Проверка мо­дели по указанному критерию может быть реализована рассмотре­нием последовательной выдачи хронологически упорядочен­ных событий в системе в моменты оконча­ния очередной работы. Однако большой объем информации, и слож­ность текущих ситуаций позволяют использовать указанную про­цедуру сопоставления для относительно малых промежутков ими­тируемого времени.

Заключительным этапом определения истинности математиче­ской модели является сравнение по статистическим критериям основных выходных параметров модели и реальной системы. Этот этап нужен не только для проверки адекватности, но и для опре­деления длительности моделирования.

Длительность моделирования рассчитывают на основе информации, получаемой непосредственно в процессе моделирования. Пусть x₁, x₂, …, x_n - случайные величины, для которых в модели осуществляется построение гистограмм, l_i, - число ин­тервалов, на которое разбивается диапазон изменения величины х_j (j=1,2,…, li). P_i,j(t) - эмпирическая частота для l-того интервала вели­чины х_j (j=1,2,…, li). Продолжительность моделирования определяется из условия:

max [P_i,j(t_k-1) - P_i,j(t_k)] < 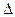(6.3)

где t_k-1, t_k - длительности двух последовательных моделируе­мых интервалов времени функционирования реаль­ной системы; величина А принимается равной 0,01. Установив длительность моделирования t = t_kна предварительном этапе, в дальнейшем можно не проверять выполнение неравенства (1), поскольку оно будет выполняться автоматически при длительности эксперимента >= t_k

В работе [48] установлено, что для получения стати­чески устойчивых характеристик функционирования мартенов­ского цеха необходимо моделировать не менее 10 суток его реальной работы.