Уравнения материального и энергетического балансов
Иногда технологический процесс можно описать совокупностью уравнений (алгебраических, дифференциальных и др.). В модели включают уравнения, описывающие законы сохранения вещества и энергии, состояние среды и ее движение, равновесие, химическую реакцию, диффузию и др.
Рассмотрим уравнения материального и энергетического балансов.
Балансы могут быть составлены как для определенного конечного отрезка времени, так и для бесконечно малого промежутка времени (мгновенные балансы). Баланс первого типа может быть использован, например, для вычисления конечной концентрации углерода в сталеплавильной ванне по уравнению:
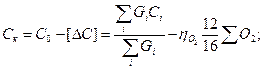(7.1)
Здесь: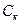 
- конечная концентрация углерода, %; 
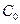- начальная концентрация углерода, %; 
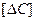- количество углерода, выгоревшего за рассматриваемый промежуток времени %; Gi - масса i-той составляющей шихты, содержащей углерод, кг; Сi - концентрация углерода в i-той составляющей шихты, %; 
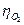- коэффициент использования кислорода, доли; 
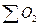- количество кислорода, поступившее из различных источников, % от садки.
Баланс второго типа можно проиллюстрировать на примере уравнения, описывающего изменение объема проточной ванны идеального перемешивания [15, с.70 - 73]. Пусть в ванну в единицу времени поступает G1 объемных единиц жидкости (приток) и уходит из нее G2 единиц (сток). Тогда скорость изменения dV/dt объема ванны (скорость накопления) будет равна
dV/dt = G1- G2 (7.2)
Это и есть уравнение мгновенного материального баланса.
Если в ванну поступает раствор, содержащий два не взаимодействующих между собой вещества А и В, концентрации которых на входе равны СA1, и СB1, а на выходе - СA2, и СB2 то уравнения мгновенных материальных балансов для каждого компонента раствора записывают следующим образом:
(d/dt)(VСA2) = G1 СA1 - G2 СA2 (7.3)
(d/dt)(VСB2) = G1 СB1 - G2 СB2 (7.4)
Если же в ванне протекает химическая реакция A + B = C + D в результате которой в единицу времени расходуется Vс молей вещества A и Vс молей вещества В и образуется по стольку же молей каждого из веществ С и D, то в этом случае система уравнений материального баланса для данного процесса будет выражена следующим образом:
dV/dt = G1- G2(7.5)
(d/dt)(VСA2) = G1 СA1 – (G2 СA2 + Vс)(7.6)
(d/dt)(VСB2) = G1 СB1 – (G2 СB2 + Vс)(7.7)
(d/dt)(VСC2) = Vс - G2 СC2 (7.8)
(d/dt)(VСB2) = Vс - G2 СD2 (7.9)
Частным случаем энергетического баланса является тепловой баланс.
Пусть, например, в результате подвода тепла 1 кг какого-либо твердого вещества, имеющего температуру Т0, превращается в пар, нагретый до температуры Т. В этом случае поступившее тепло Q будет выражено так:
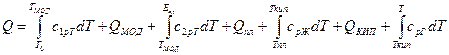(7.10)
Здесь c1рт, c2рт, cрж, cрг - теплоемкости вещества в твердом, жидком и газообразном состояниях, Дж/(кг.К); Qмод, Qпл и Qкип — теплота перехода вещества из одной модификации (в твердом состоянии) в другую, а также теплоты плавления и кипения, Дж/кг.
Поскольку теплоемкости вещества являются функциями температуры, в выражения для вычисления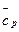 
нужны среднеинтервальные теплоемкости;
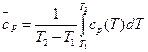(7.11)
Если известны исходные данные, уравнение теплового баланса может быть, например, использовано для расчета конечной температуры вещества.
Кроме материального и энергетического балансов в физике известны и балансы других видов. В частности, для получения математического описания процесса может оказаться полезным рассмотрение баланса импульса потока. Используя это уравнение, Л. М. Ефимов [16] получил формулу для вычисления глубины внедрения жесткой струи газа в жидкость.
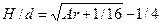(7.12)
d –диаметр кратера, равный диаметру струи, м; Н - максимальная глубина проникновения струи, м; Ar – модифицированный критерий Архимеда, в котором линейный параметр заменен на d;
При больших значениях Ar это выражение имеет своим асимптотическим приближением известную формулу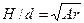 
полученную также Л. М. Ефимовым на основании экспериментальных данных И. Г. Казанцева.
Дата добавления: 2015-10-05; просмотров: 1310;