Корреляционный и регрессионный анализ

Корреляционный анализ. Использование теории корреляции для установления наличия, формы и силы связи между двумя или несколькими случайными величинами носит название корреляционного анализа. Корреляционный анализ выполняется в следующей последовательности: на основании статистических данных составляется корреляционная таблица. С помощью данных корреляционной таблицы вычисляется коэффициент корреляции и затем корреляционное отношение. По величине коэффициента корреляции и корреляционного отношения судят о форме связи (прямолинейная или криволинейная) и о силе связи. Затем на основании данных корреляционной таблицы строят эмпирическую кривую регрессии и по ее виду подбирают ближайшую теоретическую кривую и математическую формулу этой кривой. Если теоретическая кривая регрессии выражается уравнением прямой (или уравнением параболы второго порядка), то определение постоянных коэффициентов этих уравнений может быть произведено по формулам (140) или (156).

Для определения параметров уравнений регрессий используется также метод наименьших квадратов.

Регрессионный анализ. В практике часто встречается необходимость в установлении связи между двумя величинами у и х, из которых х является переменной, но не случайной величиной, принимающей в каждой новой серии опытов вполне определенное значение. Величина же у является случайной величиной, имеющей нормальное распределение с постоянной дисперсией s², не зависящей от х, но с переменным центром распределения 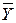, изменяющимся для каждого нового значения х. Таким образом, 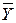является функцией х, т. е. на каждое изменение неслучайной величины х случайная величина у реагирует своим средним значением 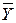. Функция 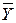= f (x) в данном случае не выражает корреляционной связи у с х, так как х не является случайной величиной, а является лишь уравнением регрессии среднего значения случайной величины у по неслучайной величине х.

Тип функции 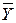= f (x) может быть линейным или криволинейным, а независимых переменных факторов может быть несколько. Мы рассмотрим только один случай, имеющий практическое применение в технологии машиностроения, когда функция 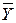= f (x) линейна и зависит только от одного переменного фактора х, т. е. выражается уравнением прямой

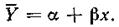
В технологии машиностроения линейный регрессионный анализ используется, например, для исследования зависимости жесткости узлов станка от нагрузки; для исследования зависимостей высоты микронеровностей на обработанной поверхности от какого-либо элемента режима резания, для исследования устойчивости технологических процессов во времени и других целей.

При регрессионном анализе тип предполагаемой функции 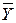= f (x) должен быть известен. В рассматриваемом случае имеется в виду, что функция выражается уравнением 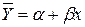. В задачи регрессионного анализа входит проверка однородности дисперсий 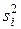величин у_i для каждого значения x_i; нахождение оценок a и b для параметров a и b теоретических линий регрессии; определение доверительных интервалов для истинных значений коэффициентов a и b; определение критерия для проверки гипотезы о линейности регрессии 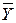на х.

Регрессионный анализ базируется на статистических данных, которые должны быть предварительно получены и систематизированы так, как указано в табл. 33.

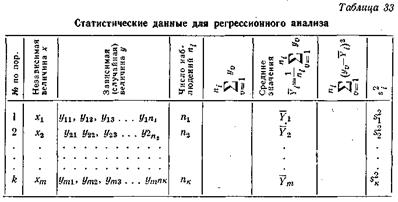
На основании данных табл. 33 строится кривая зависимости 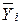от x_i. Для этого по оси абсцисс откладываются значения x_i, а по оси ординат — значения 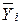. Линия, соединяющая точки пересечения 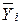и x_i, и будет эмпирической кривой связи 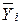с x_i.

Эмпирическая кривая связи 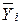с x_i в рассматриваемом случае должна приближаться к прямой, выражаемой уравнением 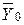= а + bх, которое определяет теоретическое значение 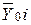для различных значений X_i. Так как вблизи точек 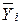полученных эмпирически, можно провести несколько прямых линий, то наилучшей из них будет та, относительно которой разброс наблюденных точек 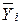будет наименьшим. Параметры а и b такой линии определяются с помощью способа наименьших квадратов. Однако прежде чем определять параметры а и b эмпирической линии регрессии, необходимо проверить гипотезу однородности дисперсий 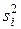для каждого нового значения x_i вычисляемых по формуле:

Проверка этой гипотезы производится по критерию G [см. формулу (127)], если n₁=n₂=…=n_k, или по критерию Q Бартлета [см. формулу (124)], когда n имеет неодинаковые значения, или путем сравнения наибольшей дисперсии с наименьшей при помощи критерия Т.

Если гипотеза однородности дисперсий подтверждается, то только при этом условии можно производить вычисление параметров а и b уравнения 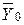= а + bх. При этом параметры а и b рассматриваются как оценки параметров a и b теоретической линии регрессии, выражаемой уравнением:

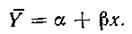
Как было указано выше, вычисление оценок а и b параметров a и b производится с помощью способа наименьших квадратов:

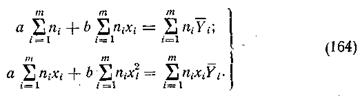
Эта система уравнений решается просто, если 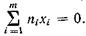Это условие всегда можно выполнить, если принять за начало отсчетов х среднюю арифметическую 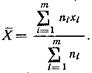. Другими словами, если перейти от прежней системы абсцисс 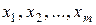, к новой системе 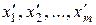, причем 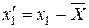, то в новой системе требуемое условие будет выполнено, так как

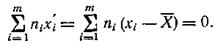
Решая систему уравнений (164) при предположении, что условие 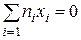выполнено, получим

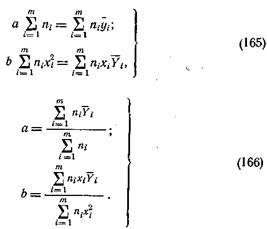
Если условие 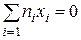не выполнено, то исходное уравнение 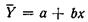следует заменить на 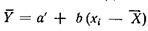, где

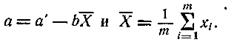
В этом случае уравнения (164) примут вид

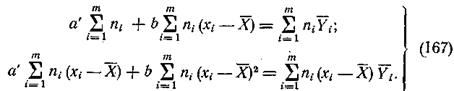
На основании уравнений (167) коэффициенты а'и b определяются по следующим формулам:

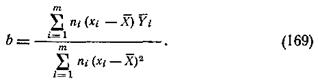
По значениям а'и b определяется коэффициент а уравнения :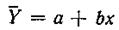

Если n₁=n₂=…=n_m, то формулы (168) и (169) примут вид

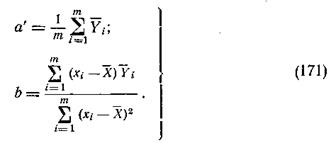
Определив коэффициенты а' и b, необходимо проверить гипотезу линейности связи 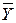с х. Для этой цели вычисляется оценка 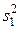дисперсии 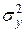распределения генеральной совокупности случайных величин y_i и оценка 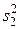дисперсии 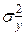рассеивания эмпирических значений 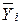относительно теоретических 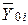, определяемых уравнением:

Дисперсия 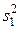вычисляется по формуле

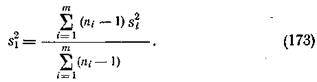
Если n₁=n₂=…=n_m, то формула (173) примет вид

Дисперсия 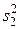вычисляется по формуле

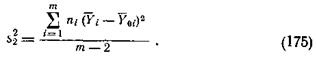
Проверка гипотезы линейности связи 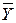с х производится при помощи критерия 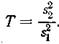. Если 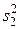значимо превышает 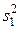, то гипотеза о линейности должна быть отвергнута.

Критические значения Т приведены в приложении 6. При пользовании этой таблицей необходимо иметь в виду, что для рассматриваемого случая

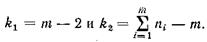. Если полученное значение Т_н будет меньше табличного значения Т, то гипотеза линейности связи 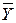с х принимается. Если Т_н > Т, то гипотеза бракуется.

Если гипотеза линейности связи 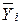с x_i подтверждается, то в этом случае можно вычислить и доверительные интервалы для a и b. Установлено, что значения коэффициентов а и b имеют нормальное распределение со средними a и b дисперсиями:

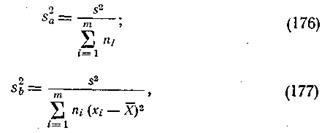
где s² — дисперсия случайных величин y_i,-, определяемая по формуле:

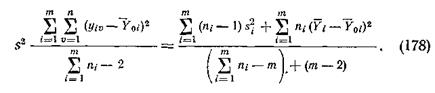
Если а и b имеют нормальное распределение, то величины 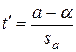и 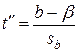подчиняются закону распределения Стюдента с 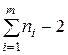степенями свободы. Поэтому, пользуясь таблицей приложения 2, можно определить точность приближенных равенств а»a и b»b в долях s_a и s_b, т. е. ,

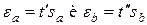Контрольные вопросы:

1. Какая связь называется стохастической? Какая связь называется корреляционной? В чем их особенности по сравнению с другими видами связей?

2. Что такое коэффициент корреляции и корреляционное отношение? Охарактеризуйте их основные свойства.

3. Что такое прямолинейная корреляционная связь?

4. Что такое криволинейная корреляционная связь?

5. Что такое множественная корреляция?

6. Что такое корреляционный анализ и в чем он заключается?

7. Что такое регрессионный анализ и в чем он заключается?

Лекция №7. Статистические методы в технологических исследованиях [6, с. 40…44; 9, с. 113 …128]

7.1. Введение

7.2. Исследование влияния технологических факторов на точность обработки и качество поверхности

7.3.Обработка экспериментальных данных по способу наименьших квадратов