Понятие о множественной корреляции
Корреляционные связи могут существовать не только между двумя, но и между несколькими признаками. Например, овальность после чистового шлифования зависит от припуска на чистовое шлифование и от овальности после предварительного шлифования; припуск на зубошлифование зависит от величины деформации заготовки шестерни после термической обработки и от погрешностей, полученных после зубонарезания и т, п,
Исследование статистических связей между многими величинами составляет предмет теории множественной корреляции. В практике механической обработки деталей на станках чаще всего встречаются случаи линейной корреляционной связи между тремя величинами или тремя факторами. Поэтому ограничимся рассмотрением простейшего случая линейной корреляционной связи между тремя величинами х, у и z, причем будем считать z величиной, зависящей от х и у. Линейная связь между z, x и у выражается уравнением

где а, b и с — постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между х и у (rxy); x и z (rxz); y и z (ryz), a также средних квадратических отклонений sx, sy, sz по формулам:
i 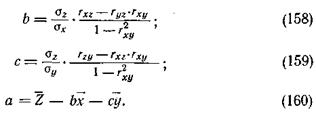
Мерой силы линейной связи между z и х, у в совокупности служит коэффициентом множественной корреляции или сводный коэффициент корреляции, который вычисляется по формуле
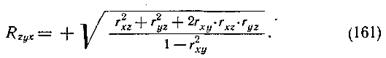


Дата добавления: 2015-10-05; просмотров: 1281;
