Криволинейная корреляционная связь
Если коэффициент корреляции 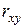 очень мал и прямолинейная связь у с х отсутствует, то возможна криволинейная связь. Для криволинейных корреляционных связей мерой силы связи является корреляционное отношение, которое определяется равенствами:
очень мал и прямолинейная связь у с х отсутствует, то возможна криволинейная связь. Для криволинейных корреляционных связей мерой силы связи является корреляционное отношение, которое определяется равенствами:
для связи у с х: 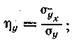
для связи х с у: 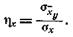
Если у с х связаны однозначной связью, то hу = 1; если связи между ними нет, то hу = 0. Аналогичные свойства относятся и к hх. Корреляционная связь между у и х будет тем теснее, чем ближе hу к 1, и тем слабее, чем hу ближе к 0.
Наиболее часто наблюдающейся в различных технических исследованиях криволинейной корреляционной связью является параболическая связь, которая выражается уравнением параболы n-го порядка. Рассмотрим случай, когда уравнение регрессии у на х имеет вид параболы второго порядка:

где а, b, с — постоянные коэффициенты;
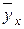 - частные средние значений у, соответствующие различным заданным значениям х.
- частные средние значений у, соответствующие различным заданным значениям х.
Для определения коэффициентов а, b, с составляются три уравнения:
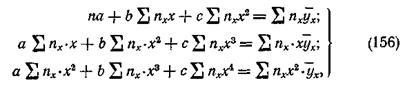
где n — общее число наблюденных значений х;
nх — частота каждого значения х.
Решение этих трех уравнений дает значение коэффициентов а, b, с.
Вычтем из уравнения (б) уравнение (а) и из уравнения (в) уравнение (б):
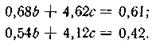
Разделим эти уравнения на коэффициенты при b:

Вычтя из уравнения (д) уравнение (г), получим
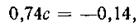
откуда
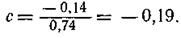
Подставляя значение с в уравнение (г), найдем
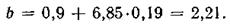
Подставляя b и с в уравнение (а), получим

Таким образом, уравнение параболической корреляционной регрессии у на х, примет следующий вид:
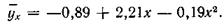
Дата добавления: 2015-10-05; просмотров: 1797;
