Коэффициент корреляции и корреляционное отношение
При изучении корреляционных связей возникает три основных вопроса: наличие связи, форма связи и сила связи. Для получения ответа на эти вопросы необходимо сначала вычислить коэффициент корреляции и корреляционное отношение.
Для вычисления коэффициента корреляции предварительно составляются корреляционные таблицы 27 и 28 результатов наблюдений. Таблицы имеет следующую структуру: по горизонтали вверху выписываются наблюденные значения случайной величины х, по вертикали слева — значения у.
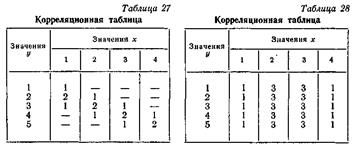
В каждом столбце корреляционной таблицы против значений х и у указываются их частоты.
По характеру таблицы можно ориентировочно судить о наличии или отсутствии корреляционной связи между у и х. Например, в табл. 27 она обнаруживается, а в табл. 28 ее нет, так как у изменяется одинаково при всех значениях х.
Имея корреляционную таблицу, подобную табл. 27, и обозначив через nху частоту некоторой пары значений х и у, вычисляют величину Сху:
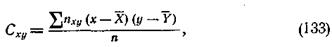
которая равна частному от деления на общее число наблюдений суммы произведений отклонений значений х и у от их средних 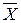 и
и 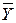 на соответствующие частоты. Эта величина Сху носит название ковариации х и у. Частное от деления величины Сху на произведение средних квадратических отклонений величин х и y, которые обозначим через sх и sy, называется коэффициентом корреляции х и у и обозначается через rху:
на соответствующие частоты. Эта величина Сху носит название ковариации х и у. Частное от деления величины Сху на произведение средних квадратических отклонений величин х и y, которые обозначим через sх и sy, называется коэффициентом корреляции х и у и обозначается через rху:

Для упрощения и облегчения вычислений ковариации Сху, а также sх и sy можно пользоваться следующими формулами:
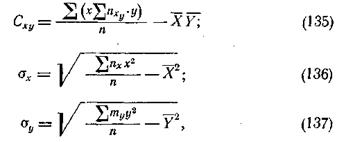
где nх и mу — частоты соответственных значений х и у.
Корреляционное отношение hу вычисляется по формуле

где sy – среднее квадратическое отклонение значений yi от средней 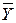 ;
;
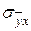 - среднее квадратическое отклонение значений частной средней
- среднее квадратическое отклонение значений частной средней 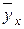 от общей средней
от общей средней 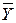 , т. е.
, т. е.
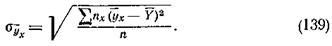
Основные свойства коэффициента корреляции и корреляционного отношения.
1. Если коэффициент корреляции rху равен плюс или минус единице, т. е.
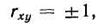
то x и у связаны точной прямолинейной связью вида
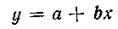
или
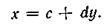
2. Если rху = 0, между х и у не может существовать прямолинейной корреляционной связи, но криволинейная возможна.
3. Чем ближе rху к ±1, тем точнее и теснее прямолинейная корреляционная связь между х и у. Она ослабевает с приближением rху к нулю.
4. Если корреляционное отношение hу = 0, то между у и х нет корреляционной связи.
5. Если hу = 1, то у связано с х однозначной связью, т. е. всякому значению х соответствует одно определенное значение у.
6. Чем ближе hу к единице, тем теснее связь у с х, чем ближе hу к нулю, тем эта связь слабее.
7. Если hу = 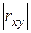 , то регрессия y на х точно линейна и обратно: если егресссия у на х точно линейна, то hу =
, то регрессия y на х точно линейна и обратно: если егресссия у на х точно линейна, то hу = 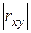 .
.
Дата добавления: 2015-10-05; просмотров: 2661;
