Проверка гипотезы равенства ряда дисперсий

Пусть имеется m выборок не равных объемов n_i,- взятых из одной или m генеральных совокупностей, имеющих нормальные распределения. При этом дисперсии этих совокупностей имеют одинаковые значения, т. е. 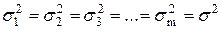, а математические ожидания могут быть и не равны друг другу.

Дисперсии выборок 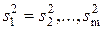, вычисленные по формуле (9), несколько отличаются друг от друга по величине. Требуется проверить гипотезу о том, что это различие дисперсий выборок носит случайный характер, и, следовательно, дисперсии генеральных совокупностей 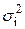, из которых взяты выборки, равны между собой, т.е. .

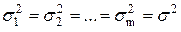При нашей гипотезе величина

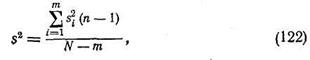
где 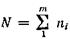; следует считать несмещенной оценкой 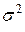. Если проверяемая гипотеза справедлива, то случайная величина

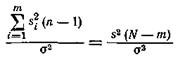
будет иметь распределение 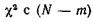степенями свободы.

Очевидно, что распределение отношения 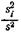при нашей гипотезе зависит лишь от n_i.

Бартлет показал, что случайная величина

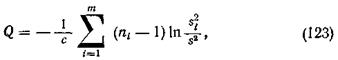
где

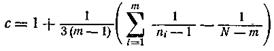
имеет распределение, близкое к распределению c² с (m -1) = k степенями свободы, если только n_i ³ 3.

Для вычисления Q пользуются следующей формулой, в которой сделан переход от натуральных к десятичным логарифмам:

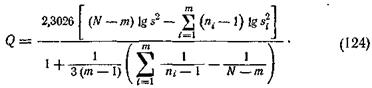
Задаваясь доверительным уровнем вероятности, например, q = 0,05 и пользуясь таблицей приложения 13, определяют верхний критический предел c² при (m -1) = k степеней свободы. Если Q <c², то гипотеза принимается, если Q > c², то гипотеза бракуется.

При равном объеме выборок проверку гипотезы однородности дисперсий проще производить упрощенным приемом, основанным на вычислении критерия G:

Критические значения G для 5%-ного уровня значимости в зависимости от объема выборок n и числа выборок m приведены в приложении 14.

Если найденное по данным выборок G_н меньше табличного G (G_н < G), то гипотеза однородности дисперсий генеральных совокупностей, из которых были взяты выборки, принимается. Если G_н > G, то гипотеза бракуется.