Проверка гипотезы равенства двух выборочных дисперсий
Пусть имеются две выборки из нормальной совокупности. Объем каждой выборки равен n1 и n2. Дисперсии этих выборок соответственно равны 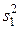 и
и 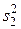 . Можно ли считать при наличии некоторых различий между величинами
. Можно ли считать при наличии некоторых различий между величинами 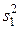 и
и 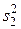 , что данные выборки принадлежат одной и той же генеральной совокупности? Или можно поставить вопрос так: произведено два опыта, из которых один опыт производился с фактором А, а другой — без него. Каждый опыт повторялся n раз. В результате обработки статистических данных получено, что дисперсия признака х в опытах с фактором А равна величине
, что данные выборки принадлежат одной и той же генеральной совокупности? Или можно поставить вопрос так: произведено два опыта, из которых один опыт производился с фактором А, а другой — без него. Каждый опыт повторялся n раз. В результате обработки статистических данных получено, что дисперсия признака х в опытах с фактором А равна величине 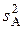 , а без него —
, а без него — 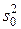 . Оказывает ли существенное влияние исследуемый фактор А на признак х? Для ответа на поставленные вопросы необходимо произвести сравнение дисперсий и оценить, является ли существенным их различие. Сравнение дисперсий производится по их отношению:
. Оказывает ли существенное влияние исследуемый фактор А на признак х? Для ответа на поставленные вопросы необходимо произвести сравнение дисперсий и оценить, является ли существенным их различие. Сравнение дисперсий производится по их отношению:
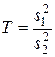 (120)
(120)
В числителе всегда ставится наибольшее значение из двух наблюденных дисперсий. Для этого отношения найден закон распределения его в бесконечной совокупности случайных независимых выборок из нормальной совокупности.
Для проверки нашей гипотезы необходимо вычислить наблюденное значение 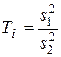 , а затем определить
, а затем определить 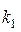 =
= 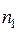 - 1 и
- 1 и 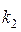 =
= 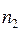 - 1), где
- 1), где 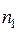 и
и 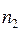 — объемы выборок, и найти для этих значений
— объемы выборок, и найти для этих значений 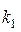 и
и 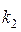 табличное значение Т.
табличное значение Т.
Если окажется, что наблюденное значение Тн равно или больше табличного Т (Тн ³ Т), то такое значение Тн в выборках из нормальной совокупности можно встретить лишь с вероятностью не более той, которая принята в качестве доверительного уровня. Если пользоваться данными таблицы приложения 6, то такой вероятностью является Р = 0,05. Так как эта вероятность очень мала, то по принципу практической невозможности маловероятных явлений надо считать, что наблюденное значение Тн отличается от табличного не случайно, а существенно, и поэтому наша гипотеза должна быть забракована. Если же окажется, что Тн < Т, то гипотеза принимается.
Случай выборок не из нормальной совокупности. Если выборки берутся из совокупностей, незначительно отличающихся от нормальных, то для сравнения дисперсий можно пользоваться критерием Т. Но если совокупность имеет распределение, значительно отличающееся от нормального, то можно сравнивать дисперсии только для больших выборок. В этом случае за критерий оценки может быть взято отношение
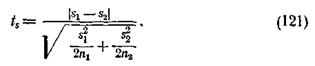
Если это отношение ts ³ 3, то расхождение между дисперсиями существенно; если ts < 3 — расхождение несущественно.
Дата добавления: 2015-10-05; просмотров: 1022;
