Проверка гипотезы равенства двух выборочных средних

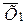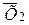Предположим, что из одной и той же генеральной совокупности взяты две выборки, которые для величины х дают средние и , отличные одна от другой. Требуется узнать, случайно или не случайно они отличаются друг от друга. Этот вопрос имеет важное значение при проведении опытов. Если расхождение между 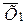и 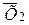будет существенно, то это может указать на ошибки в опытах или в методике их выполнения, тогда как случайность их расхождения указывает на отсутствие таких ошибок.

Рассмотрим два возможных случая: 1) выборки берутся из нормальной генеральной совокупности и 2) выборки берутся из совокупности, которая не подчиняется закону нормального распределения или когда закон распределения генеральной совокупности неизвестен.

Для первого случая оценка расхождения двух выборочных средних производится при помощи критерия t Стюдента.

Случай выборок не из нормальной совокупности. Если выборка взята из генеральной совокупности, распределение которой не следует закону нормального распределения, то оценка расхождения двух выборочных средних возможна лишь приближенная.

Для этой цели также определяется величина t, причем t вычисляется так же, как и в предыдущем случае в зависимости от объема выборок.

Если окажется, что t ³3, то с большой вероятностью (которая, однако, остается неопределенной) можно считать, что средние различаются существенно друг от друга и, наоборот, при t < 3 расхождение между с большой вероятностью можно считать несущественным, случайным.