Проверка гипотезы случайности выборки

Для описания и изучения свойств генеральной совокупности по выборке из нее необходимо, чтобы выборка была представительной, т. е. была бы репрезентативной. Репрезентативной может быть только случайная выборка.

Для проверки гипотезы случайности выборки может быть использовано два способа: способ последовательных разностей и способ числа и длины серий. Если можно допустить, что в течение наблюдений центр распределения величины х постепенно меняется, но дисперсия остается постоянной, то для проверки гипотезы «случайности» выборки является удобным и вполне приемлемым способ последовательных разностей.

Способ последовательных разностей заключается в следующем: по наблюденным значениям x_i выборки, расположенным в последовательности их наблюдения: x₁ , x₂, x₃, …, x_n, образуем n - 1 разностей между соседними членами:

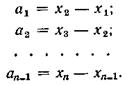
Можно доказать, что если выборка взята из генеральной совокупности с параметрами 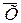и s², то математическое ожидание величины a² будет равно:

Так как состоятельной и несмещенной оценкой математического ожидания является средняя арифметическая, то взяв среднюю арифметическую из величин 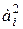и разделив ее на два, мы получим несмещенную оценку s² по данным выборки, которую обозначим с²:

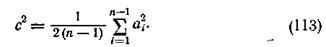
С другой стороны, для обычной несмещенной оценки s² имеем

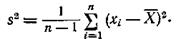
Таким образом, мы имеем две несмещенные оценки s²: с² и s².

В связи с указанным для оценки «случайности» выборки при наличии возможности смещения центра рассеивания (при неизменном s) целесообразно использовать критерий t:

При этом малые значения t следует считать указывающими на неверность гипотезы «случайности» выборки.

При n > 20 критерий t будет иметь нормальное распределение, если выборки будут действительно случайны. Поэтому критическая область для t, отвечающая q % уровню значимости при n > 20, будет определяться неравенством

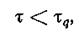
где

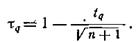
Способ длины и числа серий. Пусть имеется последовательность, в которой наблюдается случайное чередование m элементов, состоящее из n₁ элементов первого рода и n₂ элементов второго рода. Если обозначить элементы первого рода буквой а, а элементы второго рода буквой b, то такую последовательность можно представить в виде чередования букв а и b, например:

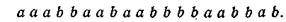
Данная последовательность состоит из 10 элементов а и 10 элементов b, т. е. n₁ = 10, n₂ = 10 и m = n₁ + n₂ = 10 + 10 = 20.

Совокупность следующих друг за другом одинаковых элементов называется серией. Число элементов, входящих в серию, называется длиной серии. В нашем примере последовательность состоит из 10 серий, в том числе имеется 5 серий из элементов а и 5 серий из элементов b. Эти серии расположены в следующей последовательности: серия а состоит из трех элементов, серия b — из двух, серия а — из двух, серия b — из одного элемента и т. д. Следовательно, длины этих серий равны: 3, 2, 2, 1 и т. д. Обозначим буквой К наибольшую длину серии любого элемента, а буквой R — общее число серий элементов а и b. В нашем примере K = 4, R = 10. Для величин К и R в случайных выборках из совокупностей с непрерывным распределением найдены законы из распределения. С помощью этих законов вычислены критические значения К и R в случайных выборках объема n = = 10…200 при доверительном уровне вероятности q = 0,05. Эти критические значения К и R используются в качестве критериев для проверки гипотезы «случайности» выборки.

Таким образом, если обозначим наблюденное значение длины серии в выборке буквой К_н, а наблюденное значение общего числа серий R_н, то для принятия гипотезы случайности выборки необходимо наличие следующих двух условий одновременно:

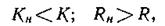
где К и R — табличные значения критерия для соответствующих значений n.

Для того чтобы гипотезу случайности отвергнуть, достаточно наличие хотя бы одного 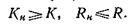из двух условий: