Понятие о стохастических и корреляционных связях

В различных исследованиях как производственного, так и лабораторного характера часто приходится изучать связи между различными количественными или качественными признаками. Если какая-либо физическая величина определяется как однозначная функция одной или нескольких величин

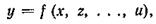
т. е. когда величина у вполне определяется значениями х, z, …, u, то такую связь величины у с величинами х, z, …, u, и мы называем функциональной. Функциональная связь может существовать и между случайными величинами. Но между случайными величинами может существовать и связь другого рода, которая проявляется в том, что одна из случайных величин реагирует на изменения другой изменениями своего закона распределения. Такая связь называется стохастической (вероятностной), или статистической, так как она обнаруживается лишь при массовом изучении признаков.

Стохастическая связь между двумя случайными величинами обычно появляется тогда, когда имеются общие случайные факторы, влияющие как на одну, так и на другую величину, наряду с другими, неодинаковыми для обеих величин, случайными факторами. Например, если

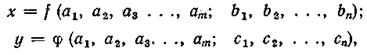
то величины х и у будут связаны между собой стохастически. Это значит, что каждому заданному значению х будет соответствовать не одно определенное значение у, а целое распределение у, которое изменяется с изменением х.

Стохастические связи могут быть весьма сложными, но наиболее простым и имеющим важное практическое значение видом стохастической связи является так называемая корреляционная связь. Корреляционная связь между двумя случайными переменными величинами выражается в том, что на изменения одной случайной величины другая случайная величина реагирует изменениями своего математического ожидания или среднего значения. Таким образом, понятие корреляционной связи является более узким, чем понятие стохастической связи, так как математическое ожидание является только лишь одним из параметров распределения и ещё не определяет закона распределения в целом.

Если имеются две статистические случайные величины х, у и если различным значениям х соответствуют определенные средние для у, которые будем называть условными средними 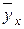, то связь между 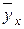и х называется корреляционной связью у с х.

Корреляционная связь может быть прямолинейной или криволинейной. В общем виде связь 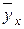с х может быть выражена уравнением

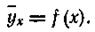
Это уравнение называют уравнением регрессии у на х, или корреляционным уравнением.