Квадратов

Исследования могут преследовать различные цели. Одной из них может быть установление функциональных или корреляционных связей между переменными величинами и выражение этих связей в виде эмпирических формул. При этом отыскание функциональных связей, например между двумя переменными величинами, носит условный характер.

В природе нет связей только между двумя величинами. Обычно каждая величина зависит от ряда других величин, которые часто заранее не известны. Поэтому задача отыскания функциональной связи между двумя переменными величинами возможна только в случае, если влияние других аргументов на изучаемую величину либо пренебрежимо мало, либо они сохраняют (хотя бы приблизительно) постоянные значения во всех наблюдениях. Последнее предположение означает, что остальные аргументы входят в функциональную зависимость в качестве постоянных параметров. Если при таких предположениях функциональная связь между переменными величинами обнаруживается, то возникает задача выбора формы связи и вида эмпирической формулы. Если функциональной связи не обнаружено, а установлено наличие корреляционной связи между переменными величинами, то и здесь возникает задача выбора формы связи и вида эмпирического уравнения корреляционной связи.

Для установления формы связи (прямолинейной или криволинейной) прибегают к графическому методу. По экспериментальным данным в системе декартовых или логарифмических координат строят эмпирическую кривую. По ее виду подбирают наиболее близкую теоретическую кривую, уравнение которой известно. Это уравнение и принимается в качестве эмпирической формулы, определяющей функциональную или корреляционную связь между изучаемыми величинами. Выбрав, таким образом, наиболее подходящий вид формулы, определяют ее параметры. Для этого пользуются способом наименьших квадратов, сущность которого заключается в следующем.

Пусть имеются некоторые переменные х, у и z, связанные между собой уравнением вида

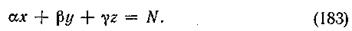
Чтобы определить неизвестные значения коэффициентов, необходимо было бы найти опытным путем значения их величины при трех различных комбинациях переменных, в результате получились бы три уравнения:

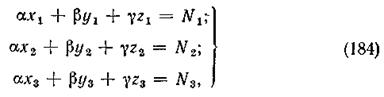
имеющих три неизвестных a, b, g, значения которых можно определить, решив систему трех уравнений. Если переменным х, у и z придать некоторые четвертые значения: х₄, у₄ и z₄ и определить опытным путем значение N₄ то окажется, что равенство (183) при значениях коэффициентов, вычисленных по уравнениям (184), удовлетворено не будет:

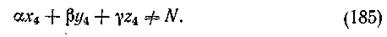
Такой результат объясняется следующим. Если бы коэффициенты были определены из уравнений (184) на основании математически точного обмера переменных х, у и z и N, равенство (183) было бы удовлетворено и при других значениях переменных х, у и z. Однако всякие измерения являются лишь относительно точными, так как экспериментатор и прибор, которым он пользуется, дают ряд неизбежных ошибок. Кроме того, значения измеряемых величин могут колебаться в каждом опыте под влиянием случайных причин. Ошибки измерений и колеблемость измеряемых величин приводят к результатам, выраженным неравенством (185).

Очевидно, значения неизвестных a, b, g надо находить в результате не трех (математически достаточных) опытов, а значительно большего количества их, чтобы получить наиболее надежные значения этих коэффициентов.

В этом случае получим систему и уравнений:

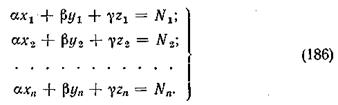
Полученная система уравнений носит название «избыточной» вследствие того, что число уравнений больше, чем число входящих в них неизвестных. Сами же уравнения называются «условными», так как они не вполне совместимы, т. е. значения неизвестных, определенные, например, из первых трех уравнений, не будут равны значениям этих же неизвестных, определенных из других трех уравнений этой системы.

Таким образом, возникает вопрос, каковы должны быть значения коэффициентов a, b, g, чтобы избыточная система уравнений удовлетворялась наилучшим образом, т. е. ошибки Е_i = N - N_i где N - расчетные, а N_i — опытные данные или

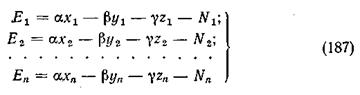
должны быть наименьшими.

Для решения поставленной задачи пользуются принципом, предложенным Лежандром и математически обоснованным в дальнейшем Лапласом и Гауссом. Согласно этому принципу из всех возможных величин a, b, g наиболее удовлетворительными будут те, при которых сумма квадратов ошибок будет наименьшая:

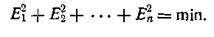
Возведение в квадрат, например, первого уравнения системы (187) дает

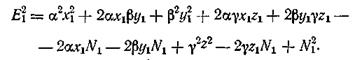
Для 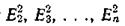получим такие же выражения с той лишь разницей, что у величин х, у, z и N будут индексы от 2 до n.

Сложив эти уравнения, получим

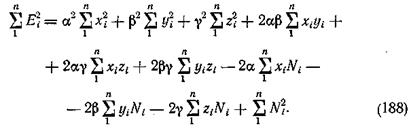
Для соблюдения условия 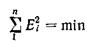необходимо, чтобы сумма частных производных по a, b, g уравнения (188) обращалась в нуль, а следовательно, и каждая из этих частных производных должна обратиться в нуль:

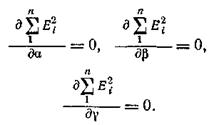
Тогда значения a, b, g, которые обращают каждую из этих производных в нуль, будут представлять собой наиболее подходящие значения коэффициентов.

Дифференцируя уравнение (188) последовательно по a, b, g, получим

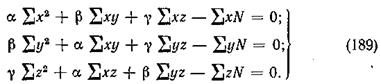
Эти уравнения носят название «нормальных». Решая их относительно a, b, g, получим наилучшие значения коэффициентов, удовлетворяющих принципу наименьших квадратов.

Сравнивая уравнения (186) и (189), нетрудно заключить, что для получения нормального уравнения, например для a, необходимо все члены из условных уравнений (186) помножить на коэффициент при a и затем почленно сложить. Так же получаются нормальные уравнения для других коэффициентов. В связи с этим отпадает необходимость прибегать каждый раз к возведению в квадрат и дифференцированию уравнений, так как все можно свести к указанным арифметическим действиям, которые выполняются механически.

Если уравнение имеет вид линейной зависимости

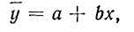
то для определения коэффициентов а и b по способу наименьших квадратов необходимо по аналогии с предыдущим составить по экспериментальным данным сумму:

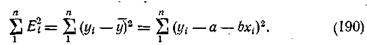
Возведя правую часть уравнения (190) в квадрат и взяв частные производные по а и b и приравняв их нулю, получим

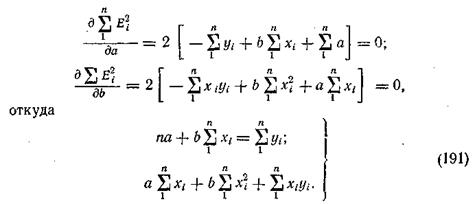
Система уравнений (191) очень легко решается, если предварительно заменить x_i на 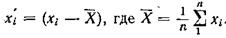. Тогда исходное уравнение примет вид

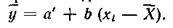
Так как 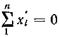, то уравнения (191) примут вид

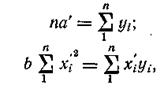
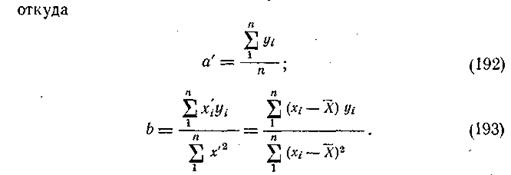
Для перехода от а' к а уравнения 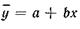служит равенство

а = а' — b .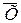

Рассмотрим еще один случай, когда уравнение имеет вид параболы третьего порядка:

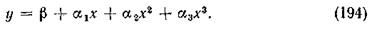
Чтобы сумма квадратов отклонений

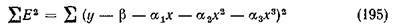
была наименьшей, необходимо выполнить четыре условия (по числу неизвестных коэффициентов a₁, a₂, a₃, b):

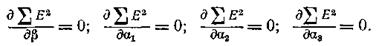
Возведя в квадрат правую часть уравнения (195) и взяв частные производные от него по a₁, a₂, a₃, b и приравняв их нулю, получим четыре нормальных уравнения:

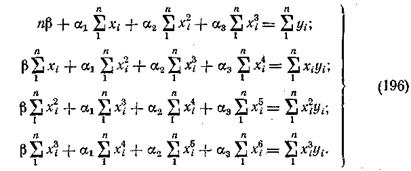
Решив эти уравнения, найдем искомую параболу третьего порядка.

Способ наименьших квадратов очень удобен для вычисления параметров уравнений линейных и параболических регрессий.

В исследованиях по резанию металлов большое распространение имеют уравнения в виде степенных функций. Чтобы определить наиболее надежные значения постоянной и показателей степеней в таких уравнениях, также пользуются способом наименьших квадратов. Для этого с помощью логарифмирования приводят степенную функцию к уравнению вида (183). Например, уравнение типа

в котором надо определить a, b и С путем логарифмирования, приводим к виду

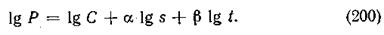
Полагая

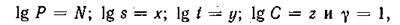
получим уравнение вида (183).

Следовательно, метод наименьших квадратов можно применить и к определению постоянной С и коэффициентов a и b в уравнении (199). При этом необходимо заметить, что ошибка [уравнение (187)] здесь представляет собой логарифм числа, а не число, т. е. наиболее подходящими значениями коэффициентов будут те, при которых сумма квадратов логарифмов величин ошибок является наименьшей.

По аналогии с предыдущим для решения задачи необходимо на основе экспериментальных данных иметь n уравнений типа (200). Прологарифмировав их, получим n условных уравнений:

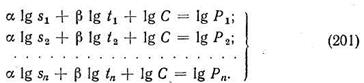
Чтобы получить нормальные уравнения, воспользуемся описанным выше механическим способом, т. е. умножим каждое из условных уравнений на коэффициент, стоящий при a, затем суммируем их; то же сделаем для b и lgС. В результате получим

для a:

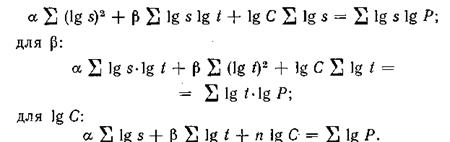
Решив систему этих уравнений, определим искомые a, b и С. По внешнему виду эмпирической кривой можно подобрать несколько теоретических кривых и, следовательно, несколько видов формул. Например, для эмпирической кривой, изображенной пунктирной ломаной линией на рис. 32, можно подобрать две формулы: для параболы второго порядка у = а + bх + сх² и для прямой у = а + bх.

Для решения вопроса о том, к какой из нескольких теоретических функций наиболее близка эмпирическая функция, необходимо вычислить для этих функций теоретические значения 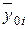для каждого наблюденного значения x_i и сравнить их с опытными значениями 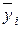. Та функция, для которой основная ошибка s₀ будет наименьшей, принимается в качестве наилучшей:

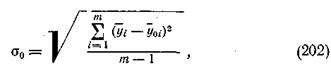
Контрольные вопросы:

1. Назовите особенности применения статистических методов в технологических исследованиях.

2. Назовите особенности применения статистических методов в исследованиях влияния технологических факторов на точность обработки и качество поверхности.

3. Как выполняется обработка экспериментальных данных по способу наименьших квадратов?

Лекция №8. Статистический анализ точности механической обработки и статистическое регулирование технологических процессов [6, 45-53; 9, с. 129…167]

8.1. Погрешности механической обработки и законы их распределения

8.2. Задачи статистического анализа точности механической обработки

8.3. Статистический анализ посредством больших выборок

8.4. Статистический анализ посредством малых выборок

8.5. Статистический анализ с помощью точечных диаграмм

8.6. Оценка точности обработки формы и взаимного расположения поверхностей и осей деталей