Выборочные функции регрессии. Метод наименьших квадратов
Функция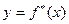 
полученная по выборке двух случайных величин X и Y и являющаяся оценкой неизвестной функции регрессии 
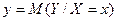называется выборочной функцией регрессии, а ее график - выборочной линией регрессии.
Метод наименьших квадратов (МНК) для нахождения функции 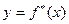применяется в случае, когда известен вид функции регрессии, зависящей от k параметров 
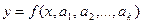, но неизвестны значения этих параметров 
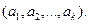Например, 
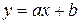, a и b неизвестны, 
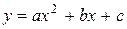, a, b, c неизвестны. 
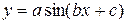, a, b, c неизвестны и т.д.
Пусть имеется выборка объема n (n>k) 
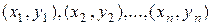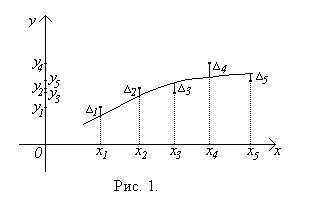
величин X и Y. Отклонением (невязкой) эмпирического значения yi от теоретического, определяемого функцией регрессии, называется разность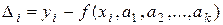 
, а суммой квадратов отклонений - функция k переменных (см. рис. 1)
.
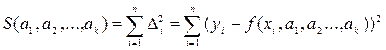Неизвестные значения параметров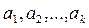 
находятся из условия минимума этой функции. Т.е., используя необходимое условие экстремума, неизвестные параметры находятся из следующей системы из k уравнений с k неизвестными.
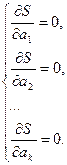(1)
Если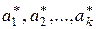 
- решение указанной системы и эти значения являются точкой минимума функции S, то искомая выборочная функция регрессии согласно МНК записывается в виде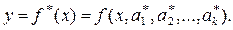 
Дата добавления: 2015-10-21; просмотров: 1128;