Лекция № 25-26. Элементы регрессионного анализа. Определение параметров линейной и нелинейной регрессии методом наименьших квадратов.
Проверка статистических гипотез
Лекция № 23-24. Проверка статистических гипотез. Критерий χ2 и его применение к проверке гипотез о виде распределения.
План.Статистическая гипотеза, критерий, критическая область и критическая точка. Ошибки первого и второго рода. Правила проверки статистической гипотезы. Критерий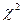 
- Пирсона для проверки гипотез о виде законов распределения дискретных и плотностей распределения непрерывных случайных величин.
Основные понятия
Статистической гипотезой называют гипотезу (предположение) о виде неизвестных случайных величин или об их параметрах. Например, «неизвестная величина имеет нормальный закон распределения» или «дисперсии двух случайных величин совпадают». Основную проверяемую гипотезу обычно обозначают через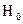 
, а альтернативную ей гипотезу, состоящую в том, что 
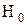не имеет места - через 
.
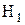Для проверки гипотез используют выборки соответствующих случайных величин. Функция наблюдаемых значений случайной величины (вариант выборки), служащая для проверки гипотезы называется критерием. Эта функция есть случайная величина вида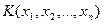 
, где 
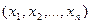- выборка исследуемой величины 
.
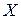На числовой оси выберем критическую область S, при попадании в которую значения критерия K, гипотеза 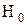отвергается. Такая область называется критической областью, а точки ее границы называются критическими точками. Чаще всего рассматриваются критические области следующего вида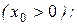 
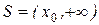- правосторонняя область,
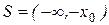- левосторонняя область,
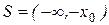
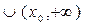- двусторонняя область.
При проверке гипотезы с помощью критерия K и области S возможны ошибки двух видов. Ошибкой первого рода называется событие, состоящее в том, что при условии справедливости гипотезы 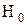, значение критерия K попадает в S, т.е. верная гипотеза 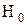отвергается. Вероятность этой ошибки называется риском первого рода:
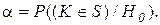
Ошибкой второго рода называется событие, состоящее в том, что при условии справедливости альтернативной гипотезы 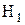, критерий K не попадает в S, т.е. неверная гипотеза 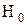принимается. Вероятность этой ошибки называется риском второго рода:
.
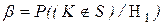В экономике эти ошибки и риски называются соответственно ошибкой (риском) продавца и покупателя.
Основной гипотезой продавца 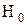является гипотеза о том, что имеющаяся у него партия товара качественная. Пусть на основании выборки из этой партии и ее проверки, продавец делает вывод, что эта партия некачественная, хотя на самом деле качество всей партии лежит в пределах нормы. В этом случае продавец уничтожает свою партию качественного товара, т.е. совершает ошибку первого рода.
Основной гипотезой покупателя 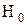является гипотеза о том, что приобретаемая им партия товара окажется качественной. Покупатель осуществляет выборку из этой партии и на основании критерия K делает заключение, что эта партия качественная, хотя качество всей партии не удовлетворяет требованиям нормы. В этом случае покупатель покупает партию некачественного товара, т.е. совершает ошибку второго рода.
В общем случае правила проверки статистической гипотезы следующие.
1. Задается максимальная величина риска первого рода - уровень значимости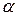 
. Это число зависит от решаемой задачи и обычно принимает значения 0,1; 0,01; 0,001 и т.д.
2. Для этого 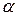определяется критическая область и ее границы – критические точки таким образом, чтобы риск второго рода 
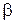был минимальным. Эта задача для каждого критерия решается заранее, и критические точки задаются с помощью таблиц.
3. Производится выборка значений случайной величины и вычисляется значение критерия. Если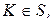 
то гипотеза 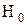отвергается, если 
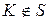то эта гипотеза принимается.
5.2. Критерий 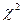- Пирсона
Этот критерий служит для проверки гипотез о виде законов распределения дискретных и плотностей распределения непрерывных случайных величин с помощью выборок таких величин достаточно больших объемов.
Случайной величиной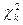 
(хи квадрат) с k степенями свободы называется величина 
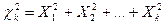, где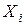 
- независимые нормальные нормированные случайные величины. С ростом k эта величина медленно приближается к нормальной случайной величине.
1) Дискретный случай. Пусть имеется дискретная величина X с конечным законом распределения вероятностей
|
| 
| 
| … | 
|
| 
| 
| … | 
|
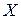
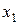
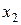
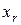
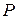
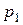
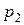
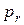
и выборка объема n этой величины со статистическим распределением частот:
| xi |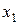
|
| … |
|
| 
| 
| … | 
|
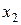
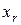
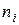
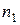
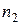
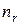
Известно, что для любой такой дискретной величины X при n стремящемся к бесконечности, величины
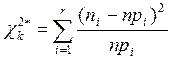
стремятся к величине 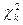с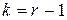 
степенями свободы. Если же закон распределения X зависит от 
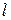параметров, которые определяются по той же выборке с помощью метода максимального правдоподобия, то число степеней свободы равно 
.
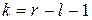Здесь мы для простоты не уточняем характер сходимости указанной величины к 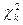. Для больших n величину 
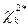можно приближенно считать равной 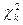, поэтому ее и используют для проверки гипотезы о том, соответствует ли исследуемая выборка случайной величине с заданным законом распределения. Порядок проверки этой гипотезы следующий.
1. Для заданного значения уровня 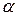и числа степеней свободы 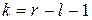по таблице критических точек распределения 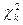определяем критическую точку 
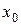для правосторонней области.
2. По статистическому распределению выборки вычисляем значение критерия .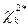
3. Если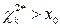 
, то проверяемая гипотеза отвергается, иначе она принимается.
Замечание. Этот критерий можно применять в случае, когда все частоты 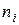статического распределения достаточно велики 
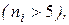в противном случае следует объединить соседние столбцы закона распределения и статистического распределения таким образом, чтобы это требование выполнялось. При этом необходимо соответственно уменьшить число степеней свободы k.
2) Непрерывный случай. Пусть проверяется гипотеза о том, что плотность случайной величины 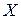имеет вид непрерывной функции 
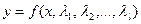, где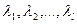 
- некоторые параметры, значения которых неизвестны. Для проверки гипотезы берется выборка объема n этой величины и по ней строится распределение частот по r промежуткам, заполняющим всю область определения 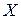вида
| 
| 
| … | 
|
|
|
|
| … |
|
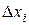
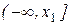
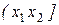
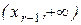
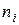
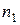
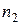
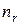
Здесь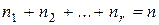 
.
По той же выборке методом максимального правдоподобия производится оценка неизвестных параметров -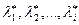 
и для этих значений находятся теоретические вероятности попадания значения величины 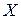в определенные выше промежутки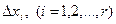 
.
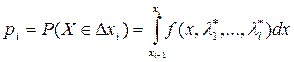Можно доказать, чтодля любой непрерывной величины 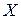при n стремящемся к 
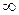, величина
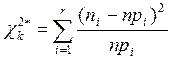
стремится к величине 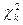с 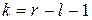степенями свободы.
Правила применения критерия для проверки указанной гипотезы те же, что и выше. Все значения ni должен быть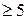 
, в противном случае следует объединить соседние промежутки.
Этот критерий можно применить, например, для проверки гипотезы о нормальном виде распределения мощностей песчаных пробок образующихся в скважинах по выборке таких мощностей объема n.
Выводы. По данной теме нами были рассмотреныпонятия статистической гипотезы, критерия, критической области и критических точек. Определено понятие ошибок первого и второго рода и правила проверки статистической гипотезы. Рассмотрен критерий 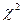- Пирсона для проверки гипотез о виде законов распределения дискретных и плотностей распределения непрерывных случайных величин.
Лекция № 25-26. Элементы регрессионного анализа. Определение параметров линейной и нелинейной регрессии методом наименьших квадратов.
План. Основные понятиякорреляционного анализа. Виды зависимостей между случайными величинами. Функции регрессии. Выборочные функции регрессии и их нахождение методом наименьших квадратов. Линейная и параболическая функции регрессии.
Дата добавления: 2015-10-21; просмотров: 950;