Статистический анализ посредством малых выборок

Метод малых выборок имеет ряд преимуществ перед методом больших выборок. Основными преимуществами его являются, во-первых, уменьшение объема вычислительных работ, во-вторых, возможность следить за динамикой изменения точности процесса во времени, чего нельзя сделать с помощью метода больших выборок. Метод больших выборок может дать представление лишь о точности и устойчивости процесса в период взятия выборки, которые могут сохраниться и в дальнейшем, если после взятия выборки условия протекания процесса не изменяются. В действительности такой неизменности производственных условий заранее предвидеть нельзя (например, при работе на прутковом автомате в течение смены производится несколько раз замена материала (смена прутка), смена инструмента в связи с износом, поднастройка станка и т. д., которые могут вносить значительные коррективы в полученные ранее параметры распределения). Метод малых выборок, если последние берут в течение всей смены регулярно через определенные промежутки времени, позволяет получить полную картину состояния процесса в течение исследуемого периода, выяснить степень его устойчивости, а также выявить причины недостаточной устойчивости процесса во времени, если она есть.

Статистический анализ малыми выборками производится следующим образом. Выборки объемом n = 5 ¸10 шт. берутся через определенные фиксированные промежутки времени (например, через 15—30 мин). Период времени для отбора проб устанавливается опытным путем и зависит от производительности станка, объема выборки и степени устойчивости технологического процесса.

Каждая выборка должна быть проверена на случайность по методу последовательных разностей, для каждой выборки нужно вычислить 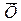и s₂. Далее необходимо для каждых двух смежных выборок проверить гипотезу однородности дисперсий выборок при помощи критерия Т. Если гипотеза однородности дисперсий выборок подтверждается, то это свидетельствует о стабильности рассеивания или о том, что сравниваемые выборки взяты из одной и той же генеральной совокупности. При подтверждении гипотезы однородности дисперсий двух выборок следует проверить гипотезу однородности двух выборочных средних по критерию t-Стюдента.

Подтверждение гипотезы равенства двух смежных выборочных средних означает, что центр настройки станка не изменился в момент взятия данной выборки и остался таким, каким был при взятии предыдущей выборки, т. е. процесс находится в стабильном состоянии. Когда гипотеза равенства двух средних выборок не подтверждается, это свидетельствует о смещении центра настройки станка во время взятия данной выборки. Так как выборки берутся через определенные промежутки времени, то при обнаружении смещения центра настройки или изменения зоны рассеивания можно определить период времени, через который наступило нарушение стабильности процесса.

Обнаружив факт нарушения стабильности процесса, можно установить и область, в которой следует искать причину этого явления. Неоднородность выборочных дисперсий, свидетельствующая о нестабильности рассеивания, указывает на то, что причину этого следует искать в станке или установочно-зажимном приспособлении, или в механических свойствах обрабатываемого материала. Например, из-за недопустимого биения шпинделя станка, недопустимого биения зажимной цанги или зажимного патрона, резкого увеличения твердости материала в каком-либо прутке может значительно увеличиться и зона рассеивания размеров.

Неоднородность выборочных средних говорит о смещении центра настройки, а значит, причиной этого может служить либо износ режущего инструмента, либо ослабление крепления инструмента, либо другая причина, но связанная с настройкой инструмента на размер.

Таким образом, беря в течение смены через определенные интервалы времени малые выборки из текущей продукции станка, вычисляя средние и дисперсии выборок путем сравнения и оценки их расхождения при помощи критериев Т и t, можно установить моменты разладок процесса и даже источники этих разладок. Устраняя причины разладок, можно привести его в состояние, когда рассеивание размеров в каждый момент времени будет носить более или менее стабильный характер. Что же касается центра рассеивания размеров, то можно добиться такого положения, что смещение его во времени будет зависеть главным образом от интенсивности размерного износа режущего инструмента и, следовательно, носить вполне закономерный характер. Другими словами, в результате статистического анализа процесса его можно привести в устойчивое состояние.

После того как процесс будет приведен в устойчивое состояние, следует установить, к какому типу точности он относится. Для этой цели необходимо параллельно с вычислением средних арифметических выборок строить кривую изменения средних для каждого номера выборки. По внешнему виду полученной кривой можно установить и тип точности изучаемого процесса.