Метод наименьших квадратов
Метод наименьших квадратов (МНК) — метод, применяемый в теории ошибок для отыскания одного или нескольких неизвестных по результатам измерений, содержащим случайные ошибки. МНК используется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным для обработки наблюдений.
В простейшем случае, когда нет систематических ошибок, а есть случайные оценки неизвестных величин, полученные с помощью МНК, то они являются линейными функциями от наблюдаемых значений — статистические оценки.
Если статистические оценки наблюдений независимы и подчиняются нормальному распределению, то МНК дает оценки неизвестных с наименьшей средней квадратичной ошибкой. В этом смысле МНК является самым лучшим среди других способов, позволяющих находить линейные несмещенные оценки.
Если мы рассматриваем слабо формализованные системы, которые трудно поддаются однозначным и точным описаниям, связь между величинами X и Y изначально корреляционная. Это связано, в частности, с тем, что Y зависит не только от X, но и от других параметров, причем такая связь часто носит случайный характер.
В этом случае, имея экспериментальные точки, задача состоит в том, чтобы приближённо свести корреляционную связь к функциональной с помощью подбора такой функции, которая максимально возможным способом близка экспериментальным точкам. Такая функция называется функцией регрессии.
Обычно вид самой функции угадывается, но она зависит от некоторых параметров. Задача статистического и корреляционного анализа состоит в нахождении этих параметров. Для этого и используется метод наименьших квадратов.
Рассмотрим случайную двумерную величину (X, Y), где 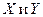 — зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением величины
— зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением величины 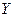 в виде линейной функции величины X:
в виде линейной функции величины X:
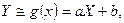
где 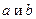 — параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них — МНК. Функцию g(x) называют среднеквадратической регрессией Y на X.
— параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них — МНК. Функцию g(x) называют среднеквадратической регрессией Y на X.
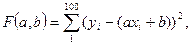
где F — суммарное квадратичное отклонение.
Подберем a и b так, чтобы сумма квадратов отклонений была минимальной. Для того, чтобы найти коэффициенты a и b, при которых F достигает минимального значения, приравняем частные производные к нулю:
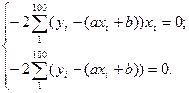
Находим a и b. Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно a и b:
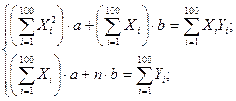
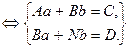 ,
,
где 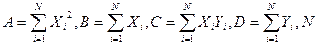 — объём выборки.
— объём выборки.
В нашем случае A = 3277; B =495; C =7188; D = 1117;N = 100.
Найдём a и b из этой системы линейных уравнений. Получим стационарную точку 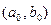 для
для 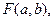 где
где 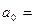 2,98;
2,98; 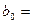 3,26.
3,26.
Следовательно, уравнение примет вид:
y=2,98x+3,26.
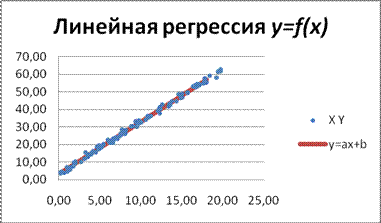
Рис. 10 Линейная регрессия y=f(x)
Построим график линейной регрессии. Для удобства наблюдения график регрессии будет на фоне диаграммы рассеивания.
Теперь построим регрессию 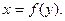
Аналогично
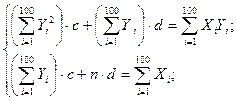
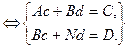 ,
,
где 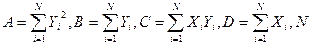 n — объём выборки.
n — объём выборки.
Теперь же A = 120716,9; B =3063,31; C =37157,64; D = 919,47; N = 100.
Найдём c и d из этой системы линейных уравнений. Получим стационарную точку 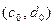 для
для 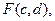 где
где 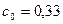 ;
; 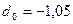 .
.
Следовательно, уравнение примет вид:
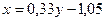 .
.
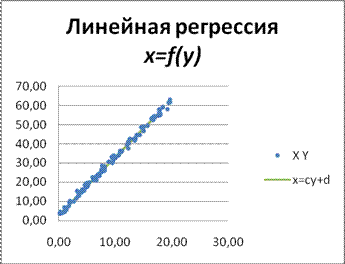
Рис. 11 Линейная регрессия x=f(y)
Теперь для наглядности изобразим обе линии линейной регрессии на диаграмме рассеивания.
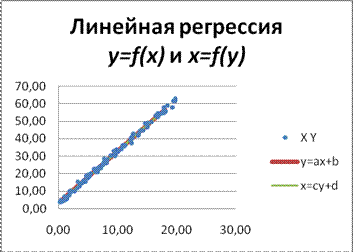
Рис. 12 Линейные регрессии y=f(x) и x=f(y)
Видно, что они практически совпадают (они должны пересекаться в районе математических ожиданий признаков 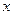 и
и 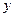 ). Зелёная линия показывает регрессию
). Зелёная линия показывает регрессию 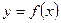 , а красная —
, а красная — 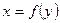 .
.
Дата добавления: 2015-09-11; просмотров: 950;
