Регрессия

Регрессия — зависимость среднего значения величины Y от другой величины X. Понятие регрессии в некотором смысле обобщает понятие функциональной зависимости y=f(x). Только в случае регрессии одному и тому же значению x в различных случаях соответствуют различные значения у.

Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов).

По форме зависимости различают:

ü линейную регрессию, которая выражается уравнением прямой (линейной функцией)

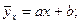
ü нелинейную (параболическую)

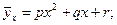
ü другие виды.

В теории вероятностей при исследовании вероятности величины Y по величине X предполагают, что при любом фиксированном значении X величина Y является случайной величиной с определенным (зависящим от значения X) условным распределением вероятностей, по которому вычисляют условное математическое ожидание:

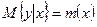
и дисперсию

.

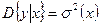Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака y от факторных (x₁, x₂,…, x_n). Основная предпосылка: только y подчиняется нормальному закону распределения, а факторные признаки (x₁, x₂,…, x_n) могут иметь произвольный закон распределения.