Метод доверительных интервалов

Рассмотренные ранее 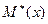, , 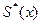, , 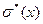, , 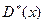, 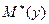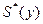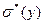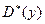являются точечными оценками, но наряду с ними при изучении выборки используются интервальные оценки, так как полезно не только построить оценку, но и охарактеризовать величину возможной при её использовании ошибки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

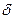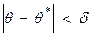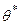Величина характеризует точность оценки, если выполняется неравенство , где — оценка некоторого параметра 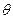генеральной совокупности. Надежностью (доверительной вероятностью) оценки 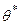по 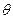называют вероятность 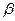, c которой осуществляется неравенство 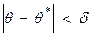. Наиболее часто задают надежность, равную 0,95; 0,9; 0,999.

Доверительным называют интервал 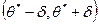, который покрывает неизвестный параметр с заданной надежностью .

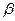Рассмотрим доверительный интервал для математического ожидания генеральной совокупности. Известен объем выборки

n = 100; 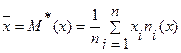= 9,1947, 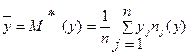= 30,6331, исправленное выборочное среднеквадратичное отклонение , .

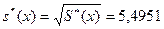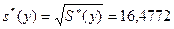Найдем доверительный интервал для оценки неизвестного математического ожидания по X с надежностями 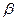= 0,95; 0,99; 0,999.

Если наблюдаемая случайная величина имеет нормальное распределение, но ее среднеквадратичное отклонение нам неизвестно, то мы можем построить доверительный интервал по распределению Стьюдента с 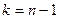степенями свободы, то есть должно быть справедливо неравенство:

;

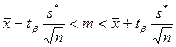где 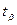определим по заданным 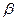и 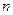. Это соотношение выражает доверительный интервал для 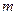, определяемый с помощью распределения Стьюдента.

Найдем доверительные интервалы для математического ожидания X.

При 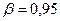; 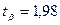: 8,1 < 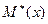< 10,3.

При 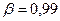; 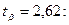7,8 < 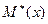< 10,6.

При 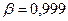; 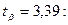7,3 < 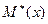< 11,1.

Заключение

В данной работе при помощи статистических методов были прослежены закономерности и связи между двумя дискретными случайными величинами: X и Y.

Для этих величин были посчитаны числовые характеристики дискретных случайных величин, построены полигоны и гистограммы распределения частот, приведены диаграммы рассеивания с линиями регрессии, а также корреляционная таблица и таблица статистической зависимости между случайными величинами X и Y.

Были проверены гипотезы о наличии линейной и полиномиальной связи между величинами X и Y, построены доверительные интервалы для математического ожидания факторного признака X.

Список литературы

1. Б. В. Петровский. Популярная медицинская энциклопедия. — Таллин: Советская Энциклопедия, 1993.

2. С. Г. Мамонов. Общая биология. — М.: Высшая школа, 1996.

3. С. Ф. Гилберт. Биология развития. — М.: Мир, 1993.

4. Г. Закс. Строение и деятельность человеческого тела. — СПб: Издательство В. В. Битнера, 1905.

5. Э. В. Семенов. Анатомия и физиология человека. — М.: АНМИ, 1995.

6. Н. А. Фомин. Физиология человека. — М.: Просвещение; ВЛАДОС, 1995.

7. Н. В. Бойчук. Курс гистологии. — Казань: Поволжский книжный центр, 1995.

8. П. Зенгбум. Молекулярная и клеточная биология. — М.: Мир, 1982.

9. Ю. Аккерман. Биофизика. — М.: Мир, 1964.

10. М. Циммерман. Физиология человека. — М.: Мир, 1996.

11. В. Е. Гмурман. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. — Изд. 7–е, стер. — М.: Высшая школа, 2001.

12. В. Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5–е, стер. — М.: Высшая школа, 2001.