Для определения p, q, r

Найдем по данным наблюдений выборочное уравнение кривой(параболической в нашем случае) линии среднеквадратичной регрессии.

Ограничимся представлением величины Y в виде параболической функции величины X:

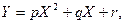
где p, q, и r — параметры, подлежащие определению. Это можно сделать с помощью метода наименьших квадратов.

Подберем параметры p, q и r так, чтобы сумма квадратов отклонений была минимальной. Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция F этих параметров:

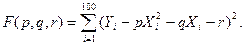
Для отыскания минимума приравняем к нулю соответствующие частные производные:

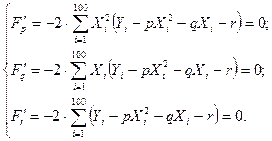
Находим p, q и r. Выполнив элементарные преобразования, получим систему трех линейных уравнений относительно p, q и r:

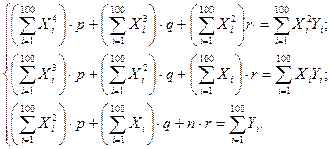
Решая эту систему методом обратной матрицы, получим: 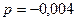; ; 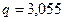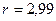. Следовательно, уравнение параболической регрессии примет вид:

y= – 0,004x²+3,055x +2,99.

Построим график параболической регрессии. Для удобства наблюдения график регрессии будет на фоне диаграммы рассеивания (см. рисунок 13).

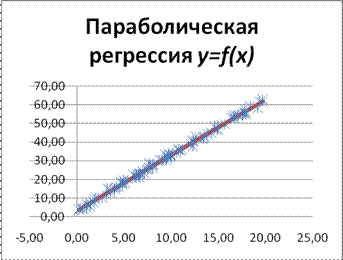
Рис. 13 Параболическая регрессия y=f(x)

Теперь изобразим линии линейной регрессии 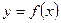и параболической регрессии на одной диаграмме, для наглядного сравнения (см. рисунок 14).

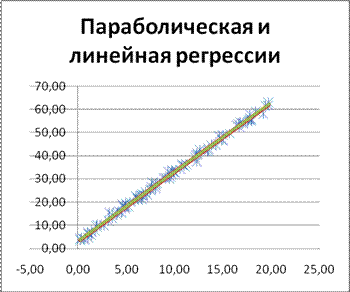
Рис. 14 Параболическая и линейная регрессии

Линейная регрессия изображена красным цветом, а параболическая — синим. По диаграмме видно, что отличие в данном случае больше, чем при сравнении двух линий линейных регрессий. Требуется дальнейшее исследование, какая же регрессия лучше выражает зависимость между x и y, т. е. какой тип зависимости между x и y.