Лекция. Изоморфты сызықтық кеңістіктер.Базистен базиске өту кезінде вектор координаттарын түрлендіру.

Екі R, R^¢ сызықты кеңістіктерін изоморфты кеңістіктер деп атайды, егер олардың элементтерінің арасында өзара бір мәнді сәйкестік бар болып, ол сәйкестік келесі шарттарды қанағаттандырар болса: х элементіне х^¢ элементінің, у элементіне у^¢ элементінің сәйкес келуінен х + у элементіне х^¢ + у^¢ элементінің, aх элементіне aх^¢ элементінің сәйкес келуі шығады.

Екі сызықты кеңістік R, R^¢ изоморфты болса, онда R жиынының нөлдік элементіне R^¢ жиынының нөлдік элементі сәйкес келеді және керісінше.

Екі изоморфты кеңістіктердің өлшемдері бірдей болады. Ендеше, барлық n - өлшемді кеңістіктер Rⁿ координаттық кеңістігіне изоморфты болады. Бұл дегеніміз, басқа n - өлшемді кеңістіктер Rⁿ координаттық кеңістігінің «көшірмесі» тәрізді деген сөз.

1 - мысал. Бірінші параграфта келтірілген 2-мысалды алайық:

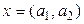түріндегі реттелген нақты сандар жиыны. Бұл жиын-ның элементтері базис болады.

Дәлелдейік. Бірінші тәсіл. Біріншіден кез келген 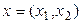элементі 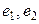элементтері арқылы өрнектеледі:

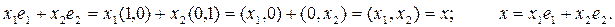
Сонымен қатар, 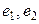элементтерінің сызықты тәуелсіздігі тек-серілуі керек. Ол үшін олардың сызықты комбинациясын нөлге теңестірейік:

,

,

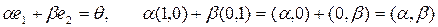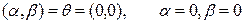яғни 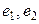элементтері сызықты тәуелсіз. Сонымен базистің екі шарты да орындалып тұр: біріншіден, 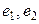элементтері сызықты тәуелсіз, екіншіден, осы элементтер арқылы сызықты кеңістіктің кез келген элементін өрнектеуге болады.

Екінші тәсіл. Берілген элементтерінен екінші ретті анықтауыш құрастырып есептейміз

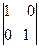= 1.

Анықтауыш нөлге тең емес, яғни берілген элементтер R² кеңістігінде базис болады.

Бұл кеңістікте базис жалғыз емес. элементтері де базис болады (тексеріңіз).

Белгілі бір элементтің әртүрлі базистердегі координаттарын есептеп көрейік.

Осы кеңістіктің 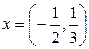элементін алайық. Бұл элементтің 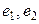базисіндегі және 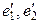базисіндегі координаталарын табайық.

; ;

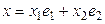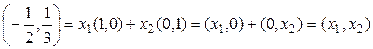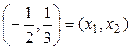. Бұдан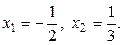

Сонымен,

.

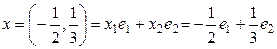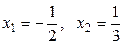сандары х элементінің 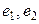базисіндегі координа-талары.

Енді екінші базисті қарастырайық

;

; ; ;

.

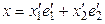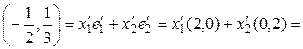
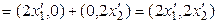
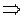
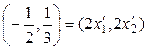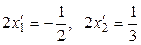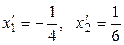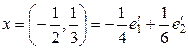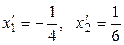сандары 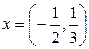элементінің 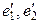базисіндегі координаталары.

Сонымен, 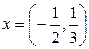элементінің әртүрлі базистегі координаталары әрқалай екенін көрдік.

Іс жүзінде элементтердің сызықты тәуелсіздігін тексеру үшін олардың сызықты комбинациясын нөлдік элементке q теңестіреміз. Осы теңдіктен сызықты комбинацияның барлық коэффициенттерінің 0 екендігі шығар болса элементтер сызықты тәуелсіз. Ал коэффициенттердің кемінде біреуі нөл емес болса, элементтер сызықты тәуелді болады.

2 - мысал. x = (-3,1,5), y = (6,-2,15) элементтері сызықты тәуелді ме?

Шешуі. Бұлардың сызықты комбинациясын нөлдік элементке q теңестіреміз

;

;

.

,

.

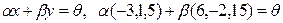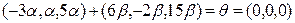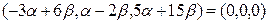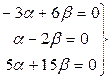
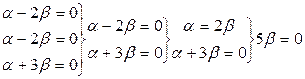Сонымен, сызықты комбинацияның коэффициенттерінің бәрі 0 екен: 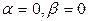. Ендеше бұл векторлар сызықты тәуелсіз болады.

3 - мысал. 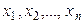элементтері сызықты тәуелсіз болып 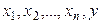элементтері сызықты тәуелді болса, онда у векторы 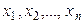элементтері арқылы өрнектелетіндігін көрсетіңіздер.

Шешуі. 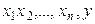векторлары сызықты тәуелді болғандық-тан, кемінде біреуі 0-ге тең емес 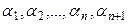сандары табылып 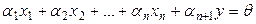теңдігі орындалады.

Мұнда 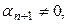өйткені 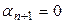болса, 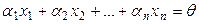теңдігін алар едік те, 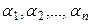сандарының кемінде біреуі 0-ге тең емес болады. Ал бұл 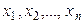элементтерінің сызықты тәуелсіз-дігіне қайшы келеді.

Сонымен 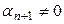. Онда 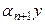мүшесін теңдіктің екінші жағына шығарамыз

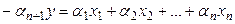
Теңдіктің екі жағында 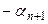санына бөлеміз де былай белгілейміз

.

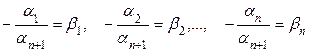Сонда у элементі 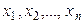элементтері арқылы сызықты өрнек-теледі екен.