Сызықты кеңістіктің өлшемі мен базисі

Сызықты кеңістіктің 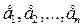элементтерінің сызықты комбинациясы деп 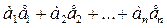- өрнегін айтамыз, мұндағы 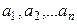- кез келген нақты сандар.

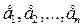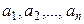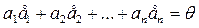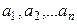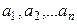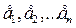Сызықты кеңістіктің элементтерін сызықты тәуелді деп айтамыз, егер кемінде біреуі нөл емес сандары табы-лып теңдігі орындалар болса, ал осы теңдіктен сандарының бәрі де нөл екендігі шығар болса,яғни онда элементтерін сызықты тәуелсіз дейміз.

Сызықты кеңістіктің сызықты тәуелсіз 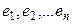элементтерін осы кеңістіктің базисі деп атаймыз, егер әрбір х элементі үшін 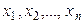сандары табылып келесі теңдік орындалар болса,

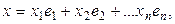
мұндағы 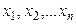сандарын х элементінің 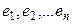базисіндегі координаталарыдеп атаймыз.

Сызықты кеңістікте n сызықты тәуелсіз элементтер бар болып, ал кез келген n+1 элементтер сызықты тәуелді болса, онда кеңістік n-өлшемді деп аталады.

Теорема 1. n-өлшемді сызықты кеңістіктегі кез-келген n сызықты тәуелсіз элементтер базис болады.

Басқаша айтар болсақ, сызықты кеңістікте базис болатын элементтердің саны сызықты кеңістіктің өлшеміне тең болады.Сызықты кеңістіктердің негізгі мысалдарын келтірейік.

1) Координаттық n - өлшемді сызықты кеңістік. Кез келген рет – ретімен орналасқан n нақты сандардың 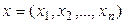түріндегі жиынын Rⁿ деп белгілейік. Амалдарды былай анықтаймыз: 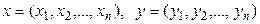элементтері үшін қосу амалы

;

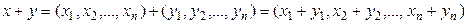элементті санға көбейту амалы

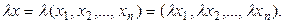
Екі элементті қосу үшін олардың сәйкес координаттарын қосады, ал элементті санға көбейткенде, элементтің барлық координаттарын сол санға көбейтеді.

Бұл жиын сызықты кеңістік болады (тексеріңіз).Rⁿ кеңістігі n- өлшемді, өйткені бұл кеңістікте

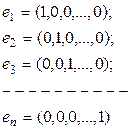
түріндегі n - элементтен тұратын сызықты тәуелсіз элементтер жүйесі (яғни базис болатын) бар. Бұл базисті кеңістіктің стандартты базисі деп атайды. Әрине, мүндағы 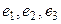элементтері де сызықты тәуелсіз, бірақ бұл үш элемент n-өлшемді кеңістікте базис бола алмайды, өйткені олардың саны аздық етеді (n-өлшемді кеңістікте базис n элементтен тұрады). Бұл кеңістікті кейде арифметикалық кеңістік деп те атайды.

2) Матрицалар кеңістігі. Өлшемі m´ n болатын матрицалар жиынында кәдімгі матрицаларды қосу және матрицаны санға көбейту амалын қарастыру арқылы сызықты кеңістік аламыз.

3) Көпмүшеліктер кеңістігі Р_n. Дәрежесі берілген n санынан аспайтын, коэффициенттері нақты сан болып келетін көпмүшеліктер жиыны. Көпмүшеліктерге кәдімгі амалдарды қолданамыз: көпмүшеліктерді қосу, көпмүшелікті санға көбейту. Кеңістіктің стандартты базисі 1, t, t², t³, …, tⁿ. Базис n+1 элементтен тұрады, яғни Р_n кеңістігі n+1 - өлшемді. Элементтері мынадай түрде жазылады

P_n = a₀ tⁿ + a₁ t^n-1 + a₂ t^n-2 + … + a_n-1 t + a_n .

Егер n – ретті анықтауыш берілетін болса, онда оның әрбір тік жолын немесе жәй жолын n - өлшемді сызықты кеңістіктің элементі ретінде қарастыруға болады. Мұндай жағдайда кеңістіктің элементтері үшін мынадай белгілеулерді пайдалануға болады. Берілген

ïАï =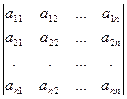

анықтауышының бірінші жәй жолының элементтерін х₁ элементінің координаттары ретінде қарастырамыз х₁ = (а₁₁, а₁₂, ..., а_1n ).Анықтауыштың басқа жәй жолдарының да элементтерін осыған ұқсас белгілейміз: х₂ = (а₂₁, а₂₂, ..., а_2n ), ..., х_n = (а_n1, а_n2, ..., а_nn ).

Теорема 2.х₁ = (а₁₁, а₁₂, ..., а_1n ), х₂ = (а₂₁, а₂₂, ..., а_2n ), ..., х_n = =(а_n1, а_n2, ..., а_nn ) элементтерінің сызықты тәуелсіз болуы үшін ïАï¹ 0 болуы қажетті және жеткілікті.

Жоғарыда n-өлшемді сызықты кеңістіктің кез-келген n сызықты тәуелсіз элементтері базис болатыны айтылды. Ендеше n-өлшемді сызықты кеңістіктіңберілген n элементінің базис болатындығын тексеру үшін, сол элементтерден анықтауыш құрастырып есептеу керек. Анықтауыш нөлге тең емес болса, берілген элементтер базис болады. Анықтауыш нөлге тең болса берілген элементтер сызықты тәуелді болғаны, яғни базис болмайды.

Қарастырылған Rⁿ кеңістігінің дербес жағдайы R² және R³ кеңістіктері.

R² кеңістігінің элементтері 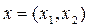түріндегі реттелген сыңарлы нақты сандар болып табылады. Бұл кеңістікте элементтері базис құрайды.

R³ кеңістігінің элементтері 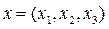түріндегі реттелген нақты сандар болып табылады. Бұл кеңістікте 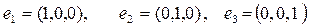элементтері базис болады, ал

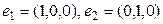элементтері базис бола алмайды, өйткені үш өлшемді кеңістікте базис үш элементтен тұрады.

Сызықты кеңістіктегі базис дегеніміз – жазықтықтағы немесе кеңістіктегі тікбұрышты координат жүйелерінің аналогы (ұқсастығы) тәріздес. Жазықтықта XOY және X¢O¢Y¢ тікбұрышты координат жүйелері берілсе, белгіленген бір нүктенің екі түрлі координаталары бар: біреуі XOY жүйесінде де, екіншісі X'O'Y' жүйе-сінде.

Сонымен қатар, бұл координаталардың бір-бірімен байланысын да біз аналитикалық геометриядан білеміз: 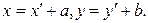Осы айтылғандарға ұқсас, сызықты кеңістіктің элементінің әртүрлі базистегі координаталары да әртүрлі болады.