Сызықты емес модель

«Димаш» атты компания номенклатуралық топтағы үш түрлі А, Б, В бұйымдарды шығарады. Осы бұйымдар бір өндіріс орнында бір жабдықтармен жасалады және жабдықтың жалпы жұмыс қоры бұйымдарды өндірген уақыттар сомасынан құралады. Сондықтан осы бұйымдардың шығару мөлшерлері бір-бірімен тығыз байланысты. Компания экономисі бір топтағы осы бұйымдардың жалпы өндіру құны, бір-бірінің өндірілген сандарымен (х_а, х_б және х_в) мынадай эмпириялық байланыста болатынын анықтады:

С = 200х_а + 600х_б + 400х_в - 100х_ах_б -50х_бх_в+ 150х_ах_в, теңге

Сонымен қатар, бұйымдардың сату құны, олардың өндірілген санына байланысты болатыны, яғни бұйымдар көп өндірілсе соғұрлым сату құндары төмендейтіні анықталды. Осы заңдылық-тардың эмпириялық модельдері статистикалық деректер арқылы тұрғызылды, яғни бір дана i-бұйымның құны:

Ц_а = 750(2 - х_а/500), теңге,

Ц_б = 1000 (2,5 - х_б/500), теңге,

Ц_в = 1500 (1,5 - х_в/500), теңге,

Өндіріс орнындағы жабдықтың қуаты, егер бұйымдардың барлық түрін бір уақытта шығаратын болса, онда олардың 500 данасын ғана шығара алады. Осы жағдайда өндіріс максимальды пайда табу үшін компанияға әрбір бұйымдарды қанша данадан шығарған тиімді екенін табу керек.

Шешу. Есептің математикалық моделін құрамыз. Есепте қойылған мақсатқа жауап беретін айнымалылар: х_а, х_б және х_в – белгілі, яғни жасалынатын А, Б, В бұйымдардың оңтайлы мөлшері. Тапқан пайданы (Z) есептейтін, мақсат функцияны тұрғызамыз.

Z = Ц_ах_а + Ц_бх_б + Ц_вх_в – C

немесе

Z = 750(2 - х_а/500) х_а + 1000 (2,5 - х_б/500) х_б + 1500 (1,5 - х_в/500) х_в –

– (200х_а + 600х_б + 400х_в - 100х_ах_б -50х_бх_в+ 150х_ах_в)

Біраз түрлендіргеннен кейін, мақсат функция мына қалыпқа келеді:

Z = 1300х_а + 1900х_б + 1850х_в – 1,5 (х_а)²– 2 (х_б)²– 3 (х_в)² +100х_ах_б +

+ 50х_бх_в – 150х_ах_в → max.

Көріп отырмыз, мақсат функция сызықты емес. Келесі кезекте шектеулер модельдерін тұрғызайық. Есепте жалғыз ғана «Үлкен» шектеу, ол – шығарылатын бұйымдардың жалпы мөл-шерінің шектеуі: х_а + х_б + х_в≤ 500 және мәндері ізделініп отырған айнымалылардың теріс болмау шарты: х_а ≥0, х_б ≥0және х_в ≥ 0. Тағы бір айрықша ескеретін жағдай, ондағы ізделініп отырған айнымалылар бүтін сандар. Модель сызықты емес болған жағдайда, бұл қызықты талап.

Сонымен математикалық модель дайын. Оны MS Excel-дің жұмыс бетіне кестелік модельге көшірейік. Біздің құрған кестелік моделіміз 2.19-суретте көрсетілген. Кестелік модельде мақсат функция формуласын енгізген кезде мұқият болғанымыз жөн (суретті қараңыз).

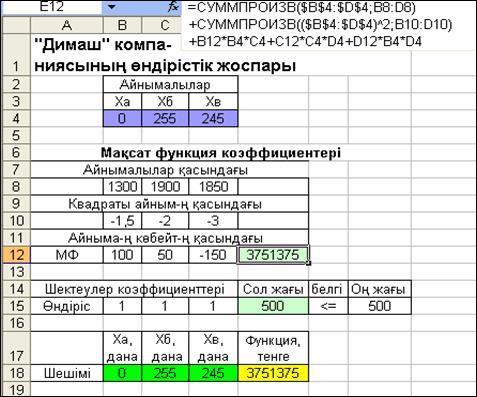
2.19-сурет. Сызықты емес модельдің шешімі

Мақсат функцияны есептеу үшін кестелік модельде оның коэффициенттері: «Айнымалылар қасындағылар», «Квадратты айнымалылардың қасындағылар» және «Айнымалылар көбейтінді-лердің қасындағылар» болып, үш топқа бөлінді. Е12 ұяда мақсат функцияның аталған коэффициенттермен формуласы, В4:D4 аралықтағы ұяларға, мәндері ізделініп отырған айнымалылар, есеп-тегі жалғыз негізгі шектеу 15-ші жолға және Е15 ұяға шектеудің сол жағының формуласы:=СУММПРОИЗВ(В15:D15;$В$4:$D$4) жазылды. Есептің шешімі, яғни 18-ші жолда В18:D18 аралықтағы ұяларда, қанша дана, сәйкесінше А, Б және В бұйымдары шығарылатыны, сол сияқты Е18 ұяда осы бұйымдарды сатқаннан кейін компанияға қанша пайда түсетіні көрсетілуі керектігі қарастырылды (2.19-сурет).

Келесі кезекте шектеулерді Поиск решенияауыстырамыз. Осы істерден кейін Поиск решения-ның сұхбаттасу терезесінің қалпы 2.20-суреттегідей болады.

Поиск решения-ның Параметры арқылы келесі сұхбаттасу терезесінде есептің моделі сызықсыз болғандықтан Линейная модель-ден флажокты алып тастаймыз. Айнымалылардың теріс болмау және автоматты масштабтау шарттарын белгілейміз (флажок қойылады). Осы әрекеттерден кейін есеп орындалуға жіберіледі. Есептің шешімі 2.19-суретте көрсетілген.

2.20-сурет. Поиск решения-ның сұхбаттасу терезесі

Есептің оңтайлы шешімінен (х_а=0) компанияға А бұйымын шығарумен айналысу тиімсіз болатынын байқаймыз. Оның есесіне Б бұйымын 255 дана, ал В бұйымын 245 дана шығару компанияға өте тиімді. Өндірістің мұндай жоспары «Димаш» компаниясына 3751375 теңге пайда түсіреді.

Сызықты емес модельдің шешімінің талдау тәсілдеріне келесі тақырыпта тереңірек тоқталамыз. Дегенмен де, сызықты емес модельді Поиск решения сұхбаттасу терезесінің әртүрлі парамет-рінде және бастапқы мәндерде біраз зерттеп көрейік.

Сызықты емес модельдерге қатысты Поиск решения-ның параметрлері: Сходимость, Оценки, Разности және Метод поиска. Аталған параметрлер қарастырып отырған сызықты емес модельге қалай әсер ететінін зерттейік. Ол үшін оларды белгілі тәсілмен іске қосамыз да, Выполнить батырмасын басып, есепті шешуге жібереміз. Сөйтіп, аталған параметрлер есептің алынған нәтижесіне ешқандай да әсер етпейтінін байқадық. Есепте анықталған айныма-лылардың бастапқы мәндерін өзгертейік. Айталық, х_а≥ 200 болсын. Оны кестелік модельге В4 ұяға енгіземіз де есепті орындауға жібереміз. Есептің жаңа шешімі 2.21-суретте көрсетілген. Жаңа шешімді 2.19-суретпен салыстырсаңыз, онда біраз өзгерістер бар екенін байқайсыз. Біріншіден А бұйымын шығарудың бастапқы мәні белгілі болған жағдайда өндіріс жоспары айтарлықтай өзгеріске ұшыраған. Екіншіден, осы әрекеттен кейін өндіріске А (248 дана) және Б (252 дана) бұйымдарын шығару тиімді болды да, пайда 6831536 теңге, яғни жуықтап алғанда ол екі еседей көбейді. Демек, қарастырылып отырған мысалдың осы өзгерісінен сызықты модельдерге қарағанда сызықты емес модельдерде айрықшылық-тар болатынын байқаймыз. Атап айтсақ, мұндай модельдерде бірнеше оңтайлы шешімдер болуы мүмкін және сіз ондай шешім-дер қаншалықты және оларды қалай табатынын алдын ала айта-алмайсыз. Дегенмен де, барлық айнымалыларға бастапқы әртүрлі мәндер тағайындап, зерттеулер жүргізу арқылы бір дәйекті шешім қабылдауға болатынына да көз жеткіздік. Біздің мысалда айныма-лыларға кезек-кезек алғашқы мән бере отырып, есепті бірнеше рет шешкенімен, осы қарастырылып отырған екі шешімнен басқа мақсат функцияны жақсартатындай шешім таба алмадық. Сондық-тан қарастырылып отырған модельдің басқа оңтайлы шешім жоқ деп тұжырымдаймыз (бірақ, бұл тұжырым сөзсіз, дәлелдеуді талап етеді).

Есептің шарты бойынша қалған екі айнымалыларға жоғарғы-дай міндеттеме жүктелінсе, яғни алғашқы модельге, бірінші кезек-те: х_б ≥200, екіншісінде: х_в ≥200, қосымша шектеулер енгізіп, есепті қайта-қайта шығарып, алғашқы екі шешімді қайтадан алдық.

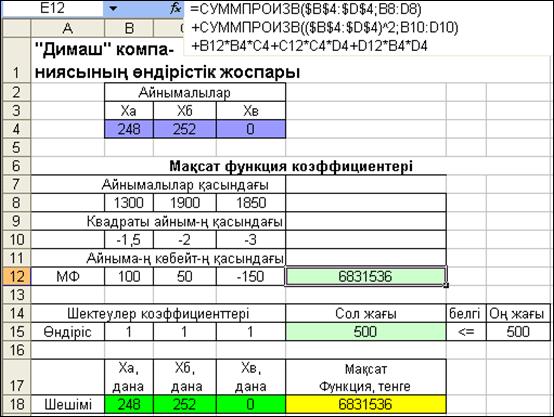
2.21-сурет. Сызықты емес модельдің жаңа шешімі

Сызықты емес модельдің параметрлерін өзгертіп, әртүрлі шешім нәтижелерін сақтап отыратын болғандықтан, сценария көмегін қолдандық. Ол үшін Поиск решения мен шешім (2.19-сурет) табылғаннан кейін сұхбаттасу терезесінде Результаты поиск решения алынады, осы терезеде Сохранить сценарий батыр-масын іске қосамыз. Сохранение сценария сұхбаттасу терезесі ашылады да, онда сценария аты енгізіледі. Біздің мысалда, ол «1-ші шешім» деп аталды. Осыдан кейін бірінші шешім сценариясы сақталады. Екінші шешімде (2.21-сурет) А бұйымын 200 данадан кем емес (х_а ≥ 200), үшінші шешімде Б бұйымын 200 данадан кем емес (х_б ≥ 200) және төртінші шешімде В бұйымын 200 данадан кем емес (х_в ≥ 200) өндіру керектігі қарастырылды, шешім нәтижелері жоғарыда баяндалған ретпен сақталынды (келесі тақырып, 2.24-сурет).

Инженерлік-техникалық сызықты емес модельдердің жалғыз ғана шешімі барлығын ерекше «белгілер» арқылы анықтауға бола-ды. Мұндай «белгілер», шектеулермен берілген айнымалылардың барлық өзгеретін аймақтарында мақсат функцияның дөңес немесе ойыс екенін анықтауға болатын, оның сыртқы түріне негізделген. Дегенмен де, көп мүшелі функция түріндегі модельдердің мұндай қасиеттерін тексеру, арнайы математикалық әдістерді қолануды талап етеді және жеңіл есеп емес.

Сонымен, сызықты емес модельдердің альтернативті шешім-дерінің ішінен ең керекті оңтайлы шешімді іздейтін қазіргі кезде бірнеше математикалық әдістері бар. Олардың көбісі шартсыз оңтайластыру есептерінде қарастырылады.