Сызықты емес модельдердің шешімін талдау

Сызықты емес модельдер шешімін талдаудың негізгі мәселесі кейбір жиі кездеспейтін жағдайлардан басқа табылған шешім шындығында оңтайлы, одан артық басқа шешім жоқ деп сендіруге және сенім білдіруге болмайды. Айнымалылардың әр-түрлі бастапқы мәнінде есепті қайта-қайта шешіп, шешім нәтиже-лерін салыстыру арқылы бір шешімге тоқталып, оны альтернативті оңтайлы шешімдердің ішіндегі ең басты оңтайлы деп тұжырым жасау әрекеті де, сізді күмәнданудан құтқармайды. Себебі, ықти-малдықтың шамасы өте аз болса да, сізде әлі де болса ең басты оңтайлы шешімді алмағаныңыз туралы, сенімсіздік қалды. Өкініш-ке орай, мұндай жағдайда қандай әдіс, әрекеттер қолдану керектігі туралы, біз қарастырған әдебиеттердің ешқайсысынан да кездестіре алмадық. Дегенмен де, айнымалылардың әртүрлі бастапқы мәнінде есепті қайта-қайта шешіп, шешім нәтижелерін салыстыру арқылы, яғни мақсат функция максимумге ізделініп отырса бір шешімде алынған оның ең үлкен (мақсат функция минимумге ізделген жағ-дайда, керісінше) мәніне тоқталып, қалған шешімдердің барлығын өшіріп, тағыда айнымалылардың келесі бастапқы басқа мәнінде есепті шешуді жалғастырып, аяғында бір дәйекті нәтижге жетуге болатынына күмән жоқ.

Сөйтіп, біздің мысалда, осындай әрекеттер жасалынып, бір тұжырымға жеттік деп есептейік.

Сызықты емес модельдер шешімін талдауда Поиск реше-ния, сызықты модельдер шешімінде алатын есептер сияқты есеп-терді қалыптастырады. Нәтижелер және шекаралар бойынша есептердің сызықтық модельдер шешімдерінде алынатын есептер-ден ешқандай айырмашылықтары болмайды. Тек, орнықтылық есеп сызықты емес модельдер шешімдерінде басқа түрде құры-лады.

2.22–суретте жоғарыда қарастырылған «Димаш» компания-сының сызықты емес моделінің бірінші шешімінің орнықтылық есебі көрсетілген. Келесі кезекте біз осы есеп бойынша шешім нәтижесіне талдау жасап көрейік.

2.22-сурет. Сызықты емес модель үшін орнықтылық бойынша есеп

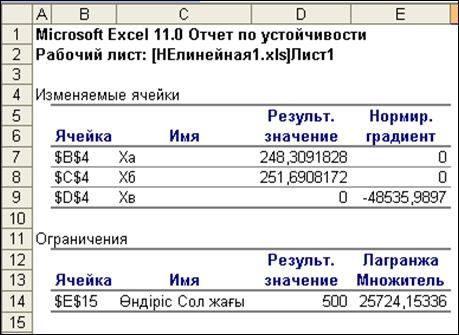
Орнықтылық бойынша есепте бізге сезімталдықты талдау үшін, Нормированный градиент бағанасындағы, Изменяемые ячейки кестесіндегі, Множитель Лагранжа бағанасындағы және Ограничения кестесіндегі мәндер қызықты.

· Нормированный градиент –мәні нөлге тең болады, егер оған сәйкес айнымалы өзінің өзгеріс аралығының шеткі шегіне жақын жатса (0 ≤ х_і ≤ а₀немесе а₁ ≤ х_і ≤ а₂).Егер х_і = 0 немесе х_і = а₀ немесе х_і = а₁ немесе х_і = а₂ болса, онда нормированный градиент (нормальдық баға) осы айнымалының өзгерістерінде (модельдің қалған параметрлері өзгеріссіз қалған жағдай-да) мақсат функция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдамдығын көрсетеді.

· Лагранжа көбейткіші – сәйкес шектеудің оң жақтағы мәнінің өзгерістерінде (модельдің қалған параметрлері өзгеріссіз қалған жағдайда) мақсат функ-ция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдам-дығын көрсетеді. Лагранжа көбейткіші оңтайлы шешімде оған сәйкес шектеу байланысты болса, тек сонда ғана нөлден басқаша.

Қарастырылып отырған екі көрсеткіштің қызметтері, оларға ұқсас, сызықтық модельдің нормальдық баға (қосымша қосалқы айнымалы) және көлеңкелік құн (қосалқы баға) көрсеткіштерінің қызметтерімен бірдей емес. Нормированный градиент – оған сәй-кес айнымалы бойынша және Лагранжа көбейткіші – оған сәйкес шектеудің оң жағы бойынша мақсат функциядан алынған туынды-лар (мақсат функция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдамдығы деп аталуының өзі, осы себепті және осы құбылыс-тың анықтамасы). Сондықтан, егер нөлдік айнымалы мәнін жоға-рылатқанда мақсат функция мәні осыншама төмендетілсе, бұл көрсеткіштерді бағалау көрсеткіштері ретінде қолдануға болады.

Сөйтіп, сызықты емес модельдің орнықтылық есебі, оның басқа есептері сияқты, шектеулердің оң жақтарынан басқа, модель-дің параметрлері туралы ештеңе де айтпайды. Сондықтан, егер модельдің басқа параметрлері арқылы оның сезімталдығын зерттеу керек болса, онда модельді керекті параметрлердің мәнінде бірне-ше рет шешуге тура келеді. Төменде осындай шешімдер нәтижесіне талдаулар жүргізілді.

Екі шешімнің нәтижелерін жоғарыда қысқаша талқыладық. Екінші шешімде пайда 6831536 теңге, яғни біріншіге (3751375 теңге) қарағанда пайда жуықтап алғанда екі еседей көбейді. Мін-детті түрде айнымалылардың біреуі оңтайлы шешімде нөлге тең болуы, екі шешімде де бірдей және бұл осы шешімдердің кемшілігі. Бірінші шешімде, егер оңтайлы шешімге х_а бір бірлігін енгізетін болсақ, онда мақсат функция мәні 23,08 мың теңгеге (бұл 2.22-суретте нормированный градиент-тің мәні) кішірейген болар еді. Осыған сәйкес, екінші шешімде, егер оңтайлы шешімге х_в бір бір-лігін енгізсек, онда мақсат функция мәні 48,536 мың теңгеге (бұл 2.23-суретте нормированный градиент-тің мәні) төмендейді. Сондықтан, егер оңтайлы шешімге енбеген әрбір бұйым 100 дана-дан кем өндірілмесін деген өндірістік қосымша талап қойылса, онда бірінші шешімде пайда 2308 мың теңгеге төмендейді (қалған пайда 943375 теңге құрайды), ал екінші шешімде пайда 4853,6 мың теңгеге төмендейді (қалған пайда 5977936 теңге құрайды). Сөзсіз, мұндай жаңа шектеулерде есепті қайта шығарған жөн. Дегенмен де, қарастырылып отырған шартта да екінші шешімнің айырмашы-лығы анағұрлым жоғары екені анық байқалады.

2.23-сурет. 2-ші шешімде алынған орнықтылық бойынша есеп

Енді шектеулерге көшейік. Біздің модельде шектеу біреу, ол өндірілетін бұйымдардың шектік саны (яғни шектеудің оң жағы бүтін сан өлшем бірлігімен «дана» деп өлшенеді). Сондықтан, осы шектеуге байланысты Лагранжа көбейткіші, қор (яғни өндірілген бұйымдардың жалпы саны) бағасы ретінде қарастырылады. Басқа сөзбен айтқанда, Лагранжа көбейткішін барлық бұйымдарды бірге қарастырғанда (біріктірген) бір бұйымнан алынатын пайда (пайда-ға бір бұйым үлесі) немесе жалпы барлық бұйымдар санының (түрлеріне байланыссыз) бір данасына шаққандағы орташа пайда деп түсіндіріледі. Аталған пайдаға бір бұйым үлесі мәнітек алын-ған шешімнің жанында кішкене аймақта сенімді, бірақ, барлық ше-шімі бола алатын аймақта бұл мән сенімді емес екенін ұмытпаған жөн.

Бірінші шешімде Лагранжа көбейткіші 13130 теңгеге, ал екіншіде – 25724 теңгеге тең. Егер өндіріс орны, қойылған шарт бойынша өндірілетін барлық бұйымдар саны 500 дананың орнына, 501 дана өндіретін болса, онда осыншама шамаға пайда мәні көтерілген болар еді. Көріп отырмыз, бұл жолы бірінші шешімге қарағанда тағыда екінші шешім ұтымды.

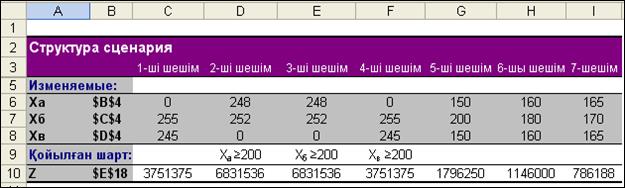
Осымен сезімталдықты талдауды бітірсе де болады. Өйткені, орнықтылық есебінде тағы да қарастыратындай ешқандай да мәлімет таба алмадық. Дегенмен де, осы жерде заңды сұрақ туады: «Барлық бұйымдар міндетті түрде өндірілетін болса, онда оларды қаншадан өндірген тиімді болар еді?» Осы сұраққа жауап беру үшін, барлық бұйымдар түрлерін 150, 160 және 165 данадан кем емес өндірілуі мінеттелген жағдайда жаңа шектеулер құрылып (х_а≥ 150; 160; 165, х_б≥150; 160; 165 және х_в≥150; 160; 165), есептің қайта-қайта шешімін тауып, нәтижесі жоғарыда баяндалған тәсілмен сценария да сақталды (2.24-сурет. 5-ші, 6-шы және 7-ші шешімдер).

Сценария кестесінен (2.24-сурет) көріп отырмыз, барлық шешімдердің нәтижелері екінші шешімге жетпейді. Сондықтан, жоғарыда келтірілген сұраққа жалғыз ғана жауап – өндірістің максимальды мүмкінділігі В бұйымын қанша өндіру керектігіне байланысты. Егер оны аз өндіру міндеттелінсе, онда өндіріс пайда-сы екінші шешімнің нәтижесіне ұмтылады да, оны көп өндірген сайын пайда төмендейді.

2.24-сурет.Сызықты емес модельдің сценариялар бойынша есебі

«Димаш» компаниясы өндірісінің сызықты емес модель-дерінің шешімдерін қысқаша талдауды қортындылайық.

1. Табылған пайда мәні бойынша өндіріске ең тиімді жоспар екінші шешімнің нәтижесінде, мақсат функцияның мына мәнінде Z = 6831536 теңге (сценариядағы 2-ші шешім) алынған: х_а = 248,

х_б =252 және х_в= 0 көрсеткіштер. В бұйымын өндіруді ұлғайтсақ, онда оның бір данасына шаққанда мақсат функция мәні 48,536 мың теңгеге қысқарады. Жалпы өндірілген бұйымдар көлемі ұлғайған сайын пайда да көбейеді, 500 данадан асқан бұйымдар санының бір бірлігінен пайда 25724 теңгеге өседі.

2. Егер өндіріске кез келген бұйымды 150 данадан кем өндірмеу керек деген міндеттеме жүктелсе, онда сызықты емес модель, мақсат функцияның мына мәнінде Z = 1796250 теңге, мынадай шешім х_а =150, х_б =200 және х_в= 150 береді. Өндіріске қойылған міндеттемеге байланысты бұл ең оңтайлы жоспар болып есептелінеді. Көріп отырмыз мұндай жоспарда екінші шешім жос-парына қарағанда пайда төрт еседей кеміген. Кез келген бұйымды өндіру көлемі туралы модельге жүктелетін міндеттеме азайған сайын В бұйымының саны міндеттемеде көрсетілген мәннен аспайды да, ал басқа бұйымдардың саны және мақсат функция мәні керісінше көбейеді. Осыдан, В бұйымды өндіруді максималь-ды қысқартсақ, пайда соғұрлым өседі деген тұжырым, өз-өзінен туындайды.

Сонымен, сызықты емес модельдің шешімін талдау қортын-дысы осындай.