Лекция. Сызықтық кеңістіктер және олардың мысалдары.Сызықтық кеңістіктің өлшемі мен базисі.

Табиғаты әртүрлі болып келе беретін х,у,z, ... элементтерінің R жиынын сызықты кеңістік деп атаймыз, егер R жиыны үшін келесі үш шарт орындалар болса:

1. R жиынының кез келген х,у элементтеріне олардың қосындысы деп аталып, былай белгіленетін z=x + y элементі сәйкес қойылған, z 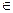R.

2. R жиынының кез келген х элементіне және кез келген l нақты санына х элементінің l санына көбейтіндісі деп аталып, былай бел-гіленетін u =lx элементі сәйкес қойылған, u 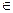R.

3. Анықталған екі амал келесі сегіз аксиоманы қанағаттанды-рады:

1°. х+у = y+x;

2°. (x+y)+z = x+(y+z);

3°. x+q = x болатындай нөлдік элемент бар ;

4°. кез келген х элементіне қарама-қарсы х¢ элементі бар және

х+х¢ = q;

5°. 1х = x;

6°. l (m х) = (lm) х;

7°. (l+m) х = l х+m х;

8°. l(х+у) = l х+l у;

Cызықтық кеңістікте нөлдік элемент жалғыз және ол 0х = q түрінде болады.

Сондай-ақ кез келген сызықты кеңістікте әрбір х элементінің жалғыз қарама-қарсы элементі бар және ол (-1) x түрінде болады.

Сызықты кеңістік элементтерін әдетте вектор деп атайды.

Есеп шығару барысында берілген жиында анықталған екі амалға назар аударып, ол амалдар үшін жоғарыдағы сегіз аксиоманың орындалуын тексеру керек. Берілген жиында екі амалдың бірі анықталмаған, яки осы сегіз аксиоманың біреуі орындалмаса, ондай жиын сызықты кеңістік болмайды.

Нақты сан өсіндегі кесінді немесе интервал, нақты сандарға қолданылатын кәдімгі арифметикалық амалдарды пайдаланар болсақ, сызықты кеңістік болмайды. Сан өсінен [0,1] кесіндісін алайық. Бұл жиында қосу амалы анықталмаған. Өйткені, осы кесіндінің екі элементі болып табылатын 0,5 және 1 сандарының қосындысы 1,5 саны бұл жиында жатпайды, яғни, қосу амалы анықталмаған.

Енді мысалдар қарастырайық.

1-мысал. R жиыны 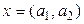түріндегі реттелген сыңарлы нақты сандардан тұрады.

Мұндағы 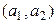мен 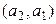әртүрлі элементтер. Бұл жиында амалдар былай анықталған

.

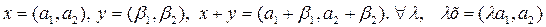Осы R жиыны сызықты кеңістік бола ма?

Шешуі. Қосу амалы алғашқы екі аксиоманы қанағаттандырады.

1. х + у = у + х, өйткені,

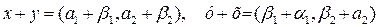
ал 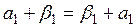, 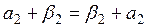себебі 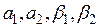дегендеріміз нақты сандар. Осы себепті 2° аксиома да орындалады. 3° аксиомаға келейік. Нөлдік элемент 0х = q түрінде болады дедік. Ендеше 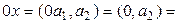q нөлдік элемент болуы керек. Бірақ, х+q = .

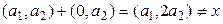Яғни 3° аксиома орындалмайды,сондықтан бұл жиын сызықты кеңістік болмайды. Осы жерде 7°-аксиоманың да орындалмайтын-дығын атап өтейік

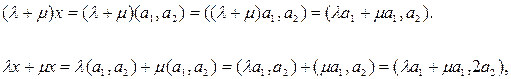
яғни .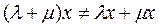

2 - мысал. Алдыңғы есепте қосу амалы сақталып, элементті санға көбейту амалын былай анықтайық

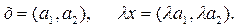
Сонда R жиыны сызықты кеңістік бола ма?

Шешуі. Бұл жағдайда R жиыны сызықты кеңістік болады. Алғашқы екі аксиоманың орындалуын жоғарыда тексердік.

3° аксиома орындалады:

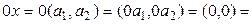q.

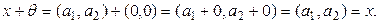
Сондай-ақ 7° аксиома да орындалады.

.

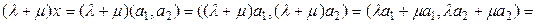
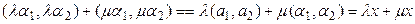5°,6°,8° аксиомалардың орындалуы да осыған ұқсас тексеріледі. Жоғарыда қарама-қарсы элемент 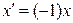түрінде болады дедік. Ендеше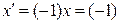 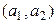= ( 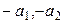) қарама-қарсы элемент болады, өйткені

.

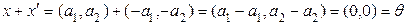Сонымен, 4° аксиома да орындалады екен.

3 – мысал. Тағы бір мысал қарастырайық. 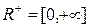жиынында екі элемент-ті қосу амалы мен элементті нақты санға көбейту амалы әдеттегі нақты сандарға қолданылып жүрген амал ретінде анықталсын. Онда бұл жиын сызықты кеңістік болмайды, өйткені 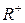жиынынан алынған кез келген элементті теріс таңбалы санға көбейткенде теріс таңбалы сан аламыз. Ал мұндай сан 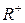жиынында жатпайды, яғни 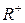жиынында элементті кез келген l нақты санына көбейту амалы анықталмаған.