Лекция. Евклид кеңістігі және олардың мысалдары. Банах кеңістігі және оның мысалдары. Сеперабельдік кеңістіктер

Екі вектордың скаляр көбейтіндісi аналитикалық геометрия курсында анықталып, кейiн бұл ұғым Rⁿ кеңiстiгiнде жалпыланған түрде, дәл айтқанда, кез-келген х = (х₁, х₂..., х_n ) және у = (у₁, у₂..., у_n ) векторлары үшiн олардың скаляр көбейтiндiсi (х,у) түрiнде таңбаланып, және

(х,у) = х₁у₁+, х₂у₂. +...х_n у_n

теңдігімен анықталғаны белгілі.

Ендi скаляр көбейтiндi ұғымын жалпы сызықтық кеңiстiктерде анықтайық.

Есызықтық кеңістік берілген болсын.

1-анықтама.Егер Е нің кез келген x,y элементтері үшін анықталған (x,y) - нақты мәнді функция

1)

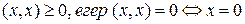
2)

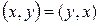
3)

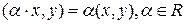
4)

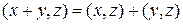
аксиомаларын қанағаттандырса, оны скаляр көбейтіндідеп атаймыз.

2-анықтама . Егер Е сызықтық кеңістігінде скаляр көбейтінді анықталған болса оны Евклид кеңістігі деп атайды .

Скаляр көбейтіндінің 1)-4) аксиомаларын пайдаланып, оның мына төмендегі қасиеттерін көрсетуге болады

;

;

;

;

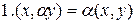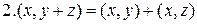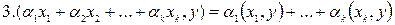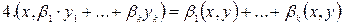Евклид кеңістігінің кез келген 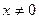элементінің скаляр (х,х) көбейтіндісі оң сан . Сондықтан , бұл (х,х) скаляр көбейтіндіден квадрат түбір - 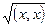алуға болады.

3-анықтама.Е - Евклид кеңістігінің 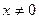элементіне сәйкес келетін (х,х) скаляр көбейтіндінің квадрат түбірін - 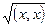оның нормасыдеп атаймыз және оны ||x|| символымен белгілеп, мына 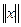= 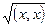формуламен өрнектейміз.

1-тұжырым.Кез келген 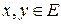үшін

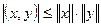
теңсіздігі орындалады.

Бұл теңсіздікті Коши – Буняковский теңсіздігі дейді.

2-тұжырым. 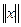= 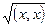өрнегі норманың аксиомаларын қанағаттандырады.

Салдары. Кез келген Евклид кеңістігі нормаланған кеңістік болады.