Гильберт кеңістігінің ішкі жиынына дейінгі арақашықтық.
Н Гильберт кеңістігі, М оның кейбір ішкі жиыны болсын.
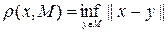 санынх элементіненМ жиынына дейінгі арақашықтық дейді.
санынх элементіненМ жиынына дейінгі арақашықтық дейді.
2-теорема.Н -Гильберт кеңістігі, L оның кез-келген ішкеңістігі болсын. Кез-келген  элементі үшін L ішкеңістігінің жалғыз y элементі табылып,
элементі үшін L ішкеңістігінің жалғыз y элементі табылып, 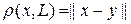 болады.
болады.
3-теорема.Н -Гильберт кеңістігі, L оның кез-келген ішкі кеңістігі болсын. Егер "  элементі үшін $yÎL ,
элементі үшін $yÎL , 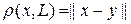 болса, онда
болса, онда
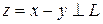 болады.
болады.
2-мысал. 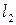 кеңістігінің
кеңістігінің 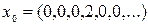 элементінен
элементінен 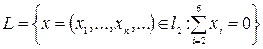 ішкеңістігіне дейінгі арақашықтықты табыңыз.
ішкеңістігіне дейінгі арақашықтықты табыңыз.
Шешуі. 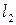 кеңістігіне тиісті болған
кеңістігіне тиісті болған 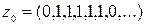 элементін қарастырайық.Егер кейбір
элементін қарастырайық.Егер кейбір 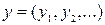 вектор L жиынына тиісті болса, онда
вектор L жиынына тиісті болса, онда
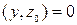 болуы қажет. Шынында да,
болуы қажет. Шынында да,
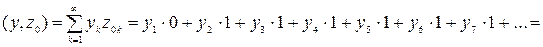
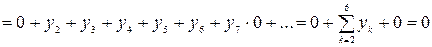
Демек, 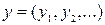 векторының L жиынына тиісті болуы шарты
векторының L жиынына тиісті болуы шарты 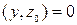 .Олай болса, z0 ^ L. Осы жерде L кеңістігіне ортогонал болатын L^ жиынында анықтап кетейік.Анықтама бойынша L^={yÎ
.Олай болса, z0 ^ L. Осы жерде L кеңістігіне ортогонал болатын L^ жиынында анықтап кетейік.Анықтама бойынша L^={yÎ 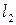 : " xÎ L: (x,y)=0 }.
: " xÎ L: (x,y)=0 }.
Бұл жиын L^={yÎ 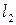 : y=a z0, aÎR} болатыны айқын.
: y=a z0, aÎR} болатыны айқын.
Лекция. Сызықтық оператор анықтамасы, өзара бірмәнді, суперпозициялы операторлар . Сызықты оператордың үздіксіздігі, шенелгендігі, нормасы. Интегралды және дифференциал операторлар. Нормаланған сызықты операторлар кеңістігі. Сызықты және нормаланған кеңістіктегі кері операторлар
Н1 және Н2 – гильберт кеңістіктері болсын делік. Егер барлық 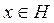 үшін
үшін
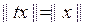 (1)
(1)
болса, онда Н1-ден Н2-ге дейін t операторы изометриялық деп аталады. Бұл 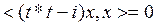 теңдігіне эквивалентті және сондықтан
теңдігіне эквивалентті және сондықтан
 (2)
(2)
болады. Бұдан шығатыны
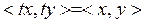 (барлық
(барлық 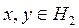 үшін) (3)
үшін) (3)
Егер t операторының бейнесі тұтас Н2-мен бірдей болса, онда изометриялық оператор унитар оператор деп аталады. (1) шартынан t операторының өзара бірмәнділігі шығатындықтан Н1-дан Н2-ге деген унитар оператордың бар болуының қажетті және жеткілікті шарты болып Н1 мен Н2 кеңістіктері өлшемдерінің бірдейлігі табылады. Керісінше, егер 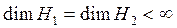 болса, онда Н1-ден Н2-ге деген кез келген изометриялық оператор унитар болады. Ақырсыз өлшемді кеңістіктер үшін бұл ұйғарым, әрине, әділ емес.
болса, онда Н1-ден Н2-ге деген кез келген изометриялық оператор унитар болады. Ақырсыз өлшемді кеңістіктер үшін бұл ұйғарым, әрине, әділ емес.
Гильберт кеңістігі Н-тағы симметриялық және унитарлық операторлар нормальдық операторлардың дербес жағдайы болып табылады. Егер t мен t* ауыстырымды болса
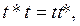 (4)
(4)
онда  операторы нормальдық деп аталады.
операторы нормальдық деп аталады.
Бұл қасиет келесіге эквивалентті:
барлық 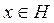 үшін
үшін 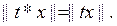 (5)
(5)
Нормальдық операторлардың маңызды қасиеті мынау:
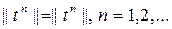 (6)
(6)
Бұдан, жеке жағдайда, спектралдық радиус
 (7)
(7)
(6) формуланың дәлелдемесін біз симметриялық t операторының жеке жағдайынан бастаймыз. Алдымен ескертеніміз
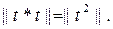 (8)
(8)
Расында да, 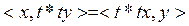 болатындықтан
болатындықтан
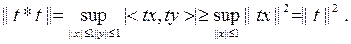
Басқа жағынан,  болатындықтан
болатындықтан  Осылайша,
Осылайша, 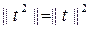 , t2 симметриялы болатындықтан
, t2 симметриялы болатындықтан  Осыған ұқсас пайымдап (6) теңдігі
Осыған ұқсас пайымдап (6) теңдігі 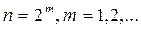 үшін әділ екенін көреміз. t операторы нормальдық, бірақ міндетті түрде симметриялық емес деп жориық. (8)-ді тағы қолданып
үшін әділ екенін көреміз. t операторы нормальдық, бірақ міндетті түрде симметриялық емес деп жориық. (8)-ді тағы қолданып 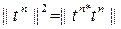 екенін аламыз. Бірақ (4) бойынша
екенін аламыз. Бірақ (4) бойынша  және
және 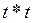 операторы симметриялық, онда
операторы симметриялық, онда  үшін
үшін 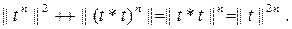 Осыдан (6)
Осыдан (6)  үшін дәлелденді. Кез келген n жағдайы үшін
үшін дәлелденді. Кез келген n жағдайы үшін 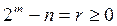 болатындай m-ді сайлаймыз. (6) формула
болатындай m-ді сайлаймыз. (6) формула 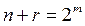 үшін әділ болатындықтан
үшін әділ болатындықтан 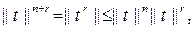 бұдан
бұдан 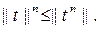 Қарама-қарсы теңсіздік айқын болған себепті (6) теңдік дәлелденді.
Қарама-қарсы теңсіздік айқын болған себепті (6) теңдік дәлелденді.
Симметриялық операторлардың маңызды мысалы болып, ортогонал проектор немесе проекциялық оператор табылады. L H-кеңістігінің кеңістік асты болсын делік. Бенио Леви теоремасы бойынша кез келген 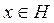 элементін
элементін 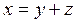 түрінде бірмәнді көрсетуге болады, мұнда
түрінде бірмәнді көрсетуге болады, мұнда 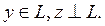
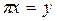 деп тұтас Н-та анықталған мәндерінің облысы L кеңістік асты болатын кейбір операторды аламыз. Бұл оператор проекциялық оператор (немесе L – кеңістікастының үстіне ортогонал проекциялау операторы) деп аталады және ол да
деп тұтас Н-та анықталған мәндерінің облысы L кеңістік асты болатын кейбір операторды аламыз. Бұл оператор проекциялық оператор (немесе L – кеңістікастының үстіне ортогонал проекциялау операторы) деп аталады және ол да 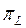 деп белгіленеді.
деп белгіленеді. 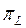 операторы нормасы бірге тең өзі түйіндес оператор және
операторы нормасы бірге тең өзі түйіндес оператор және  шарты идемпотентті қанағаттандырады.
шарты идемпотентті қанағаттандырады.
Бәрінен бұрын, π сызықтық оператор, із жүзінде, егер 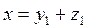 және
және  мұнда
мұнда 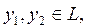 ал
ал 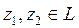 болса, онда
болса, онда 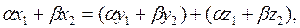 мұнда
мұнда  бұдан
бұдан 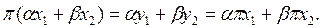 Әрі қарай у пен z-тің ортогоналдығынан,
Әрі қарай у пен z-тің ортогоналдығынан, 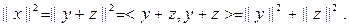 Сондықтан,
Сондықтан,  яғни кез келген х үшін
яғни кез келген х үшін 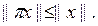 Бұдан
Бұдан 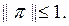
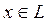 болғандықтан
болғандықтан 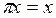 және сол себепті,
және сол себепті, 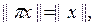 онда
онда 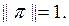
π - өзі түйіндес оператор екенін көрсетейік. х1 мен х2 тағы екі элемент, у1 пен у2 олардың L-дің үстіне проекциясы болсын делік. 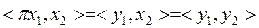 екенін аламыз. Осыған ұқсас,
екенін аламыз. Осыған ұқсас, 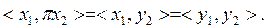 Сондықтан,
Сондықтан, 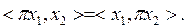 Ең соңында, кез келген
Ең соңында, кез келген 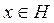 үшін
үшін 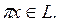 Сол себепті кез келген
Сол себепті кез келген 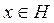 үшін
үшін  яғни
яғни 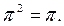
Кері ұйғарым да, анығында, кез келген өзі түйіндес идемпотенттік π операторы кейбір L кеңістік үстіне ортогонал проекциялау операторы екені де әділдігін көрсетейік. 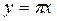 түріндегі элементтердің L жиынын қарайық. Мұнда х тұтас Н-ты түгендейді. π операторының аддитивтілігі мен біртектілігі бойынша жиыны сызықтық көп бейне болады. L тұйық екенін оңай көрсетуге болады. Іс жүзінде
түріндегі элементтердің L жиынын қарайық. Мұнда х тұтас Н-ты түгендейді. π операторының аддитивтілігі мен біртектілігі бойынша жиыны сызықтық көп бейне болады. L тұйық екенін оңай көрсетуге болады. Іс жүзінде 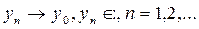 болсын делік.
болсын делік. 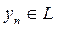 болғандықтан кейбір
болғандықтан кейбір 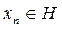 үшін
үшін 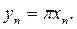 Сондықтан
Сондықтан  π операторының үзіліссіздігі нәтижесінде,
π операторының үзіліссіздігі нәтижесінде, 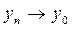 - ден
- ден  шығады.
шығады. 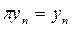 теңдігін ескеріп
теңдігін ескеріп 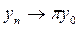 екенін аламыз. Сондықтан,
екенін аламыз. Сондықтан,  және
және 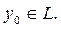
π операторының өзі түйіндестігі мен 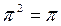 шартынан шығатыны
шартынан шығатыны 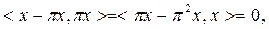 яғни
яғни  Енді L кеңістікастының өзінің анықтамасынан π осы кеңістікасты үстіне проекциялау операторы екені шығады және дәлелдеу керегі осы еді. L сондай, тек сондай,
Енді L кеңістікастының өзінің анықтамасынан π осы кеңістікасты үстіне проекциялау операторы екені шығады және дәлелдеу керегі осы еді. L сондай, тек сондай, 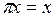 болатындай
болатындай 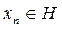 нүктелерінен тұратынын ескертеміз.
нүктелерінен тұратынын ескертеміз.
Дәлелденген, жеке жағдайда, π мен бірге і-π-да проекциялық оператор екені шығады.
Проекциялық операторлардың кейбір қарапайым қасиеттерін атайық. Егер 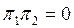 болса π1 мен π2 екі проекторы ортогонал деп аталады. Бұл шарт
болса π1 мен π2 екі проекторы ортогонал деп аталады. Бұл шарт 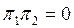 шартына пара-пар, себебі егер
шартына пара-пар, себебі егер 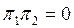 болса, онда
болса, онда 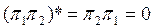 және керісінше.
және керісінше.
π1 мен π2 проекторлары ортогонал болуы үшін сәйкес L1 және L2 кеңітік астылары ортогонал болуы қажетті және жеткілікті.
Іс жүзінде, егер 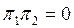 болса, онда
болса, онда 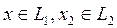 үшін
үшін

Керісінше, егер 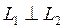 болса, онда кез келген
болса, онда кез келген 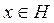 үшін
үшін  болады және сондықтан
болады және сондықтан 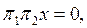 яғни
яғни 
3-лемма. 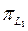 және
және  екі проекторының қосындысы проектор болуы үшін осы операторлардың ортогонал болуы қажетті және жеткілікті. Егер осы шарт орындалса, онда
екі проекторының қосындысы проектор болуы үшін осы операторлардың ортогонал болуы қажетті және жеткілікті. Егер осы шарт орындалса, онда 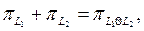 бұдан
бұдан 
Жеткіліктілігі 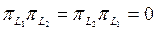 болсын делік. Сонда
болсын делік. Сонда 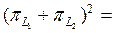
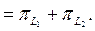 Сол себепті
Сол себепті 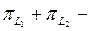 проекциялық оператор.
проекциялық оператор.  шарты бойынша L1 және L2 кеңістікастылары ортогонал. Егер
шарты бойынша L1 және L2 кеңістікастылары ортогонал. Егер 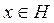 болса, онда
болса, онда
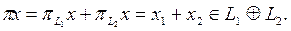 (9)
(9)
Егер, әрі қарай, 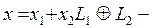 дегі элемент болса, онда
дегі элемент болса, онда 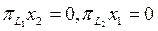 теңдіктерін ескеріп, алатынымыз
теңдіктерін ескеріп, алатынымыз
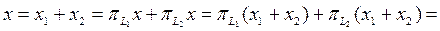
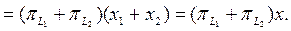 (10)
(10)
(9) бен (10) теңдіктерінен π  дің үстіне проекциялық оператор екені шығады.
дің үстіне проекциялық оператор екені шығады.
4-лемма. 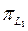 және
және  проекциялық екі оператордың көбейтіндісі проекциялық оператор болуы үшін
проекциялық екі оператордың көбейтіндісі проекциялық оператор болуы үшін 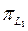 және
және  операторлары ауыстырымды болуы қажетті және жеткілікті. Егер осы шарт орындалса, онда
операторлары ауыстырымды болуы қажетті және жеткілікті. Егер осы шарт орындалса, онда 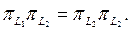
Дәлелдеме. Қажеттілігі.  өзі түйіндес оператор болса, онда
өзі түйіндес оператор болса, онда 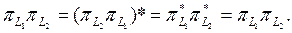
Жеткіліктігі. Егер 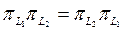 болса, онда
болса, онда  өзі түйіндес оператор. Сонымен қатар,
өзі түйіндес оператор. Сонымен қатар,
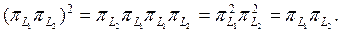
және сондықтан π – проекциялық оператор.
х Н-тағы кез келген элемент болсын делік. Сонда 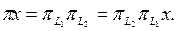 L1-ге де, L2-ге де, яғни
L1-ге де, L2-ге де, яғни 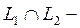 де жатады.
де жатады.
Енді 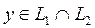 болсын делік. Сонда
болсын делік. Сонда 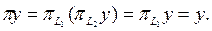 Осының бәрі π -
Осының бәрі π - 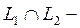 нің үстіне проекциялық оператор екенін білдіреді.
нің үстіне проекциялық оператор екенін білдіреді.
Егер 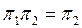 болса, онда проекциялық π2 операторы проекциялық операторының бөлігі деп аталады. Түйіндес операторға көшу арқылы бұл анықтаманың
болса, онда проекциялық π2 операторы проекциялық операторының бөлігі деп аталады. Түйіндес операторға көшу арқылы бұл анықтаманың 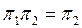 анықтамасына пара пар екеніне сенеміз. Анықтамадан тікелей шығатыны
анықтамасына пара пар екеніне сенеміз. Анықтамадан тікелей шығатыны  операторы
операторы  операторының сонда, тек сонда ғана бөлігі болады, егерде L2 кеңістікасты L1 кеңістікастынығ бөлігі болса ғана.
операторының сонда, тек сонда ғана бөлігі болады, егерде L2 кеңістікасты L1 кеңістікастынығ бөлігі болса ғана.
 проекциялық операторы
проекциялық операторы 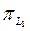 проекциялық операторының бөлігі болуына барлық
проекциялық операторының бөлігі болуына барлық 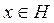 үшін
үшін 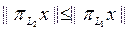 теңдігі орындалуы қажетті және жеткілікті.
теңдігі орындалуы қажетті және жеткілікті.
Іс жүзінде,  тен шығатыны
тен шығатыны 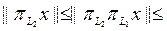
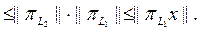 Керісінше, егер осы шарт орындалса, онда кез келген
Керісінше, егер осы шарт орындалса, онда кез келген 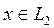 үшін
үшін 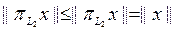 екенін аламыз және
екенін аламыз және 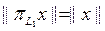 теңсіздігі де әділ болатындықтан
теңсіздігі де әділ болатындықтан 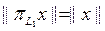 . Сол себепті, кез келген
. Сол себепті, кез келген 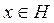 үшін
үшін 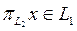 және, демек,
және, демек,  яғни
яғни  дәлелдеу керегі осы еді.
дәлелдеу керегі осы еді.
5-лемма. Екі проекциялық оператордың 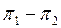 айырымы сонда, тек сонда ғана проекциялық болады, егер
айырымы сонда, тек сонда ғана проекциялық болады, егер 
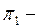 дің бөлігі болса. Егер осы шарт орындалса, онда
дің бөлігі болса. Егер осы шарт орындалса, онда 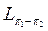
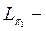 дегі
дегі 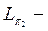 ге ортогонал толықтауыш болады.
ге ортогонал толықтауыш болады.
Дәлелдеме. Қажеттілігі. Егер 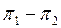 проекциялық оператор болса, онда
проекциялық оператор болса, онда  де проекциялық оператор. Бірақ онда 3-лемма бойынша
де проекциялық оператор. Бірақ онда 3-лемма бойынша 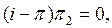 яғни
яғни 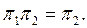
Жеткіліктілігі. 
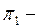 дің бөлігі болсын. Сонда
дің бөлігі болсын. Сонда 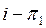 және
және  ортогонал, әрі 3-лемма бойынша
ортогонал, әрі 3-лемма бойынша 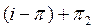 проекциялық оператор, және, содан,
проекциялық оператор, және, содан, 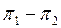 операторы да проекциялық.
операторы да проекциялық. 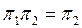 шартынан ең соңында
шартынан ең соңында 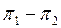 мен
мен  ортогонал екені шығады. Бірақ онда сол 3-лемма бойынша
ортогонал екені шығады. Бірақ онда сол 3-лемма бойынша 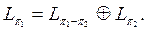
Дата добавления: 2015-09-29; просмотров: 2449;
