Лекция. Гильберт кеңістігі және оның мысалдары. Гильберт кеңістігінде Фурье қатары

1-анықтама. Н – Евклид кеңістігі берілген болсын.Егер Н толық, ақырсыз өлшемді болса, оны Гильберт кеңістігі дейді.

Айталық, Н Гильберт кеңістігінде { e_k }- ортонормал жүйе берілген болсын,

2-анықтама. 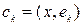- сандарын хÎ Н элементінің Фурье коэффициенттері , ал 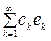қатарын Фурье қатарыдейді.

Фурье қатарының жинақтылыққа зерттейік. Ол үшін қандайда бір a_k тұрақтыларын алып, 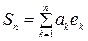қосындыны зерттейік:

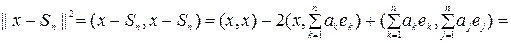
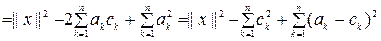
Демек,

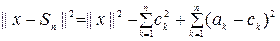
Егер бұл теңдікте 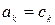болса, онда

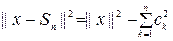
болады. Бұдан 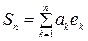түріндегі қосындыларының ішінде х элементке ең жақын тұратыны Фурье қатарының n – дербес қосындысы болатыны көрініп тұр.

Егер 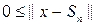екенін есепке алсақ , бұдан

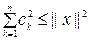
теңсіздігі келіп шығады. Бұл теңсіздікте 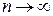шекке өтсек,онда

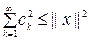
теңсіздігіне ие боламыз. Бұл теңсіздіктіБессель теңсіздігі дейді.

Егер

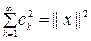
теңдігі орынды болса, оны Парсеваль теңдігі дейді.

3-анықтама.Егер{ e_k } жүйеде Н - Гильберт кеңістігінің кез келген х элементі үшін Парсеваль теңдігіорындалса бұл жүйені тұйық жүйе дейді.

Егер{ e_k } жүйе тұйық болса , онда

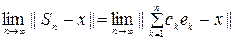
болады, яғни х тің Фурье қатары сол элементке жинақталады.

1-теорема( Рисс-Фишер) . Н -Гильберт кеңістігінде { e_k } ортонормал жүйе және 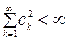шартты қанағаттандыратын с_k – сандар тізбегі берілген болсын.

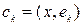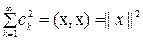Онда Н кеңістігіне тиісті х элементі табылып: с_k -лар х элементінің Фурье коэффициенттері , яғни және болады.

Енді Гильберт кеңістігінің кейбір ішкі кеңістіктерін қарастырамыз.

Гильберт кеңістігі нормаланған кеңістік болғандықтан, оның ішкі кеңістіктерін нормаланған кеңістіктердегі сияқты анықтаймыз.

Демек, Н тің ішкі кеңістігі - тұйық болған сызықтық кеңістіктер.

1-мысал. Н гильберт кеңістігінен кез келген z элементін аламыз. Егер

М ={x: xÎ Н , x^z }, яғни Н тің z элементке ортогонал болған барлық нүктелері жиыны болса, онда М жиыны Н тің ішкі кеңістігі болады.

Шешуі.Алдымен М сызықты жиын болатынын көрсетейік. x,yÎ М , "lÎR болсын. Онда

(x+y,z)= (x, z )+(y,z)=0 Þ x+yÎ М;

(l x,z)= l ( x,z)=0 Þ l xÎ М;

Енді М нің тұйық болатынын дәлелдейміз. М тұйық Û "x_n Î М және x_n® а Þ а Î М, яғни М ді тұйық дейміз, егер де М жиынына тиісті " x_n тізбегінің шегі а сол жиынға тиісті болса.

Айталық, x_n Î М және x_n® а болсын.

Онда, || x_n- а||²=( x_n- а, x_n- а)® 0, n® ¥,

Þ |( x_n- а, x_n- а)|= || x_n||²-2(а, x_n) +||a||² Þ|(а, x_n)|£ || x_n||²-||a||².